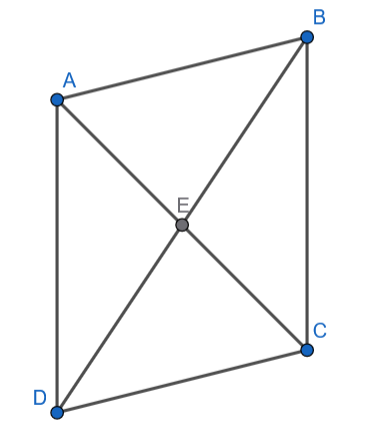
Czworokąt jest równoległobokiem, gdy jego przekątne przecinają się w połowie:
Trójkąty AED i BEC są przystające z cechy KBK: – kąty naprzemianległe, więc:
Jeśli przekątne przecinają się w połowie, to czworokąt jest równoległobokiem, więc ma dwie pary równych boków:
Trójkąty AED i BEC są przystające z cechy BKB: – kąty wierzchołkowe, więc: Trójkąty AEB i DEC są przystające z cechy BKB: – kąty wierzchołkowe, więc:
To kończy dowód.
