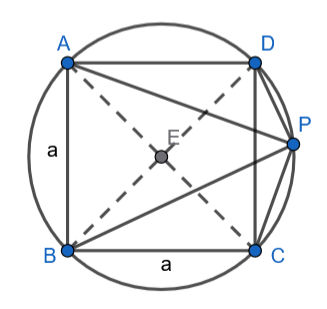
Trójkąty BDP i ACP są prostokątne, ponieważ kąty BPD i APC są oparte na takim samym łuku jak kąt środkowy BED i AEC – który ma miarę .
Z twierdzenia Pitagorasa:
Niezależnie od położenia punktu P, suma kwadratów odległości punktu P od wierzchołków tego kwadratu ma stałą wartość równą poczwórnemu kwadratowi boku kwadratu.
To kończy dowód.
