Narysuj wykres funkcji:
![]() . Wykorzystaj interpretację graficzną współczynników tej funkcji.
. Wykorzystaj interpretację graficzną współczynników tej funkcji.
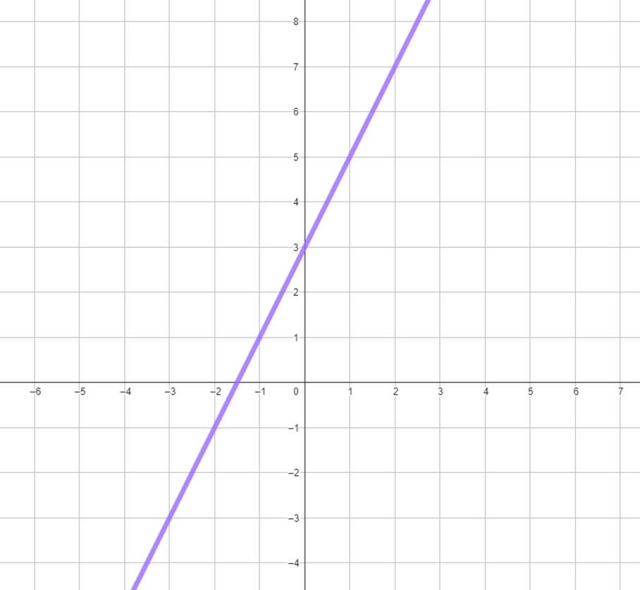

Wzór ogólny funkcji liniowej to
![]() . Skorzystaj z własności współczynników a i b. Współczynnik kierunkowy a mówi nam o przebiegu funkcji liniowej. Jeżeli zwiększymy x o 1 jednostkę, to y zmieni dokładnie o a jednostek. Współczynnik b mówi nam, w którym miejscu dana funkcja liniowa przecina się z osią y. Będzie to punkt
. Skorzystaj z własności współczynników a i b. Współczynnik kierunkowy a mówi nam o przebiegu funkcji liniowej. Jeżeli zwiększymy x o 1 jednostkę, to y zmieni dokładnie o a jednostek. Współczynnik b mówi nam, w którym miejscu dana funkcja liniowa przecina się z osią y. Będzie to punkt
![]() . Dla
. Dla
![]() ,
,
![]() , więc co każdy jeden x, wartość y wzrośnie o
, więc co każdy jeden x, wartość y wzrośnie o
![]() . Skoro
. Skoro
![]() , oznacza to, że wykres przetnie oś y w punkcie
, oznacza to, że wykres przetnie oś y w punkcie
![]() .
.

Zadanie 1.4
341Zadanie 1.5
341Zadanie 1.7
341Zadanie 1.8
342Zadanie 1.9
342Zadanie 1.10
342Zadanie 1.11
342Zadanie 1.13
343Zadanie 1.14
343Zadanie 1.15
343Zadanie 1.16
343Zadanie Prosto do matury 4
343Zadanie 2.4
351Zadanie 2.5
351Zadanie 2.6
351Zadanie 2.7
351Zadanie 2.8
351Zadanie 2.9
351Zadanie 2.10
351Zadanie 2.11
352Zadanie 2.16
352Zadanie 2.17
352Zadanie 2.19
352Zadanie 2.21
353Zadanie 2.22
353Zadanie 2.28
353Zadanie 2.29
354Zadanie 2.30
354Zadanie Prosto do matury 3
354Zadanie Prosto do matury 5
354Zadanie 3.4
360Zadanie 3.5
360Zadanie 3.6
360Zadanie 3.7
360Zadanie 3.9
361Zadanie 3.10
361Zadanie 3.11
361Zadanie 3.14
361Zadanie 3.16
362Zadanie 4.4
366Zadanie 4.5
367Zadanie 4.6
367Zadanie 4.7
367Zadanie 4.8
367Zadanie 4.9
367Zadanie 4.10
368Zadanie 4.12
369Zadanie 4.13
369Zadanie 5.5
377Zadanie 5.6
377Zadanie 5.7
377Zadanie 5.8
377Zadanie 5.9
377Zadanie 5.11
377Zadanie 5.12
378Zadanie 5.13
378Zadanie 5.14
378Zadanie 5.16
378Zadanie 5.17
378Zadanie 5.18
378Zadanie 5.19
378Zadanie 5.20
378Zadanie 5.21
379Zadanie 5.22
379Zadanie 6.6
384Zadanie 6.8
384Zadanie 6.9
384Zadanie 7.5
390Zadanie 7.6
391Zadanie 7.7
391Zadanie 7.8
391Zadanie 7.12
392Zadanie 8.32
397Zadanie 8.36
397Zadanie 8.37
397Zadanie 8.38
397Zadanie 8.39
398Zadanie 8.40
398Zadanie 8.41
398Zadanie 8.48
398Zadanie 8.49
399Zadanie 8.56
400Zadanie 8.57
400Zadanie 8.58
400
