Sporządź wykres funkcji
![]() . Na podstawie wykresu podaj liczbę rozwiązań równania
. Na podstawie wykresu podaj liczbę rozwiązań równania
![]() ,
,
![]() .
.
Krok 1:
![]()
Krok 2:
![]()
Krok 3:
![]()
Krok 4:
![]()
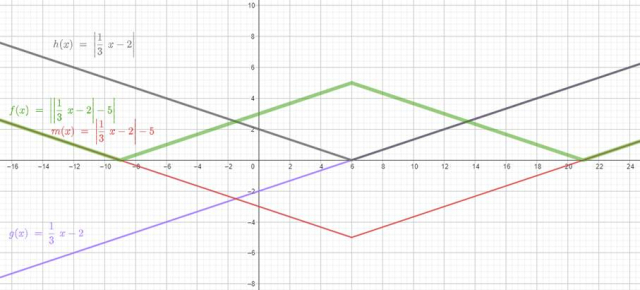
Dla
![]() – 0 rozwiązań
– 0 rozwiązań
Dla
![]() – 2 rozwiązania
– 2 rozwiązania
Dla
![]() – 3 rozwiązania
– 3 rozwiązania
Dla
![]() – 4 rozwiązania
– 4 rozwiązania

Skorzystaj z odpowiednich przekształceń funkcji liniowej, aby uzyskać funkcję
![]() :
:
Krok 1: prosta funkcja liniowa.
Krok 2: obłóż funkcję liniową wartością bezwzględną (czyli odbij symetrycznie względem osi x tą część wykresu, która znajduje się pod osią x).
Krok 3: przesuń wykres o 5 jednostek w dół.
Krok 4: obłóż funkcję liniową wartością bezwzględną.
Następnie wyznacz, ile rozwiązań ma
![]() , dla
, dla
![]() . Polega to na policzeniu, ile różnych rozwiązań ma funkcja
. Polega to na policzeniu, ile różnych rozwiązań ma funkcja
![]() w różnych przedziałach na osi y.
w różnych przedziałach na osi y.

Zadanie 1.4
341Zadanie 1.5
341Zadanie 1.7
341Zadanie 1.8
342Zadanie 1.9
342Zadanie 1.10
342Zadanie 1.11
342Zadanie 1.13
343Zadanie 1.14
343Zadanie 1.15
343Zadanie 1.16
343Zadanie Prosto do matury 4
343Zadanie 2.4
351Zadanie 2.5
351Zadanie 2.6
351Zadanie 2.7
351Zadanie 2.8
351Zadanie 2.9
351Zadanie 2.10
351Zadanie 2.11
352Zadanie 2.16
352Zadanie 2.17
352Zadanie 2.19
352Zadanie 2.21
353Zadanie 2.22
353Zadanie 2.28
353Zadanie 2.29
354Zadanie 2.30
354Zadanie Prosto do matury 3
354Zadanie Prosto do matury 5
354Zadanie 3.4
360Zadanie 3.5
360Zadanie 3.6
360Zadanie 3.7
360Zadanie 3.9
361Zadanie 3.10
361Zadanie 3.11
361Zadanie 3.14
361Zadanie 3.16
362Zadanie 4.4
366Zadanie 4.5
367Zadanie 4.6
367Zadanie 4.7
367Zadanie 4.8
367Zadanie 4.9
367Zadanie 4.10
368Zadanie 4.12
369Zadanie 4.13
369Zadanie 5.5
377Zadanie 5.6
377Zadanie 5.7
377Zadanie 5.8
377Zadanie 5.9
377Zadanie 5.11
377Zadanie 5.12
378Zadanie 5.13
378Zadanie 5.14
378Zadanie 5.16
378Zadanie 5.17
378Zadanie 5.18
378Zadanie 5.19
378Zadanie 5.20
378Zadanie 5.21
379Zadanie 5.22
379Zadanie 6.6
384Zadanie 6.8
384Zadanie 6.9
384Zadanie 7.5
390Zadanie 7.6
391Zadanie 7.7
391Zadanie 7.8
391Zadanie 7.12
392Zadanie 8.32
397Zadanie 8.36
397Zadanie 8.37
397Zadanie 8.38
397Zadanie 8.39
398Zadanie 8.40
398Zadanie 8.41
398Zadanie 8.48
398Zadanie 8.49
399Zadanie 8.56
400Zadanie 8.57
400Zadanie 8.58
400
