Narysuj wykres funkcji
![]() . Następnie na podstawie wykresu określ monotoniczność funkcji
. Następnie na podstawie wykresu określ monotoniczność funkcji
![]() .
.
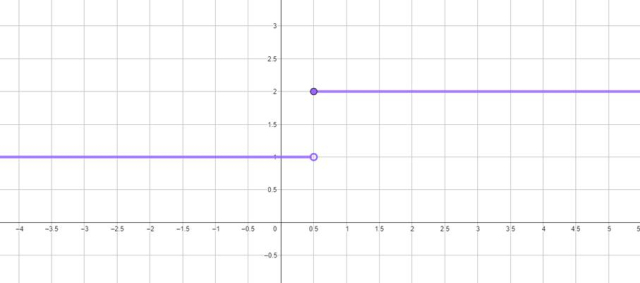
Funkcja jest stała (i równa 1) dla
![]()
Funkcja jest stała (i równa 2) dla
![]()
Funkcja jest niemalejąca.

Narysuj podane fragmenty funkcji w odpowiadających im przedziałach. Pamiętaj przy zaznaczaniu krańców prostej, że jeżeli punkt ten należy do dziedziny, oznaczamy go wypełnionym kółkiem, a jeżeli nie należy, oznaczamy to kółkiem niewypełnionym. Z racji, że funkcja jest w całej swojej dziedzinie jest stała, i w punkcie
![]() funkcja „przeskakuje” z wartości niższej do wartości wyższej (czyli rośnie), podana funkcja jest niemalejąca – ponieważ w żadnym miejscu nie maleje.
funkcja „przeskakuje” z wartości niższej do wartości wyższej (czyli rośnie), podana funkcja jest niemalejąca – ponieważ w żadnym miejscu nie maleje.

Zadanie 1.4
341Zadanie 1.5
341Zadanie 1.7
341Zadanie 1.8
342Zadanie 1.9
342Zadanie 1.10
342Zadanie 1.11
342Zadanie 1.13
343Zadanie 1.14
343Zadanie 1.15
343Zadanie 1.16
343Zadanie Prosto do matury 4
343Zadanie 2.4
351Zadanie 2.5
351Zadanie 2.6
351Zadanie 2.7
351Zadanie 2.8
351Zadanie 2.9
351Zadanie 2.10
351Zadanie 2.11
352Zadanie 2.16
352Zadanie 2.17
352Zadanie 2.19
352Zadanie 2.21
353Zadanie 2.22
353Zadanie 2.28
353Zadanie 2.29
354Zadanie 2.30
354Zadanie Prosto do matury 3
354Zadanie Prosto do matury 5
354Zadanie 3.4
360Zadanie 3.5
360Zadanie 3.6
360Zadanie 3.7
360Zadanie 3.9
361Zadanie 3.10
361Zadanie 3.11
361Zadanie 3.14
361Zadanie 3.16
362Zadanie 4.4
366Zadanie 4.5
367Zadanie 4.6
367Zadanie 4.7
367Zadanie 4.8
367Zadanie 4.9
367Zadanie 4.10
368Zadanie 4.12
369Zadanie 4.13
369Zadanie 5.5
377Zadanie 5.6
377Zadanie 5.7
377Zadanie 5.8
377Zadanie 5.9
377Zadanie 5.11
377Zadanie 5.12
378Zadanie 5.13
378Zadanie 5.14
378Zadanie 5.16
378Zadanie 5.17
378Zadanie 5.18
378Zadanie 5.19
378Zadanie 5.20
378Zadanie 5.21
379Zadanie 5.22
379Zadanie 6.6
384Zadanie 6.8
384Zadanie 6.9
384Zadanie 7.5
390Zadanie 7.6
391Zadanie 7.7
391Zadanie 7.8
391Zadanie 7.12
392Zadanie 8.32
397Zadanie 8.36
397Zadanie 8.37
397Zadanie 8.38
397Zadanie 8.39
398Zadanie 8.40
398Zadanie 8.41
398Zadanie 8.48
398Zadanie 8.49
399Zadanie 8.56
400Zadanie 8.57
400Zadanie 8.58
400
