Udowodnij, że dla funkcji
![]() i
i
![]() nie istnieje taka wartość parametru m, aby te funkcje były do siebie prostopadłe.
nie istnieje taka wartość parametru m, aby te funkcje były do siebie prostopadłe.
Założenia:
![]()
![]()
Teza:
Nie istnieje taka wartość m, dla której wykresy funkcji
![]() i
i
![]() są prostopadłe.
są prostopadłe.
Dowód:
Załóżmy, że proste
![]() i
i
![]() są prostopadłe. Wtedy:
są prostopadłe. Wtedy:
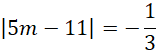
Co jest sprzeczne.
Zatem
![]()
Nie istnieje takie m, aby te proste były prostopadłe.
Co należało udowodnić.

Najpierw załóż, że wykresy funkcji są wobec siebie prostopadłe. Dwie proste
![]() oraz
oraz
![]() są prostopadłe wtedy, gdy z pomiędzy ich współczynnikami zachodzi zależność:
są prostopadłe wtedy, gdy z pomiędzy ich współczynnikami zachodzi zależność:
![]() . Żeby proste były prostopadłe, wartość
. Żeby proste były prostopadłe, wartość
![]() musiałaby być ujemna, co jest niemożliwe.
musiałaby być ujemna, co jest niemożliwe.

Zadanie 1.4
341Zadanie 1.5
341Zadanie 1.7
341Zadanie 1.8
342Zadanie 1.9
342Zadanie 1.10
342Zadanie 1.11
342Zadanie 1.13
343Zadanie 1.14
343Zadanie 1.15
343Zadanie 1.16
343Zadanie Prosto do matury 4
343Zadanie 2.4
351Zadanie 2.5
351Zadanie 2.6
351Zadanie 2.7
351Zadanie 2.8
351Zadanie 2.9
351Zadanie 2.10
351Zadanie 2.11
352Zadanie 2.16
352Zadanie 2.17
352Zadanie 2.19
352Zadanie 2.21
353Zadanie 2.22
353Zadanie 2.28
353Zadanie 2.29
354Zadanie 2.30
354Zadanie Prosto do matury 3
354Zadanie Prosto do matury 5
354Zadanie 3.4
360Zadanie 3.5
360Zadanie 3.6
360Zadanie 3.7
360Zadanie 3.9
361Zadanie 3.10
361Zadanie 3.11
361Zadanie 3.14
361Zadanie 3.16
362Zadanie 4.4
366Zadanie 4.5
367Zadanie 4.6
367Zadanie 4.7
367Zadanie 4.8
367Zadanie 4.9
367Zadanie 4.10
368Zadanie 4.12
369Zadanie 4.13
369Zadanie 5.5
377Zadanie 5.6
377Zadanie 5.7
377Zadanie 5.8
377Zadanie 5.9
377Zadanie 5.11
377Zadanie 5.12
378Zadanie 5.13
378Zadanie 5.14
378Zadanie 5.16
378Zadanie 5.17
378Zadanie 5.18
378Zadanie 5.19
378Zadanie 5.20
378Zadanie 5.21
379Zadanie 5.22
379Zadanie 6.6
384Zadanie 6.8
384Zadanie 6.9
384Zadanie 7.5
390Zadanie 7.6
391Zadanie 7.7
391Zadanie 7.8
391Zadanie 7.12
392Zadanie 8.32
397Zadanie 8.36
397Zadanie 8.37
397Zadanie 8.38
397Zadanie 8.39
398Zadanie 8.40
398Zadanie 8.41
398Zadanie 8.48
398Zadanie 8.49
399Zadanie 8.56
400Zadanie 8.57
400Zadanie 8.58
400
