Sporządź wykres podanej funkcji.
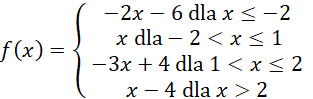
Następnie korzystając z wykresu oceń prawdziwość podanych zdań.
A. Funkcja
![]() przyjmuje wartość najmniejszą równą -2 dla dwóch argumentów:
przyjmuje wartość najmniejszą równą -2 dla dwóch argumentów:
![]() .
.
B. W przedziale
![]() funkcja
funkcja
![]() jest rosnąca.
jest rosnąca.
C. W przedziale
![]() funkcja
funkcja
![]() jest rosnąca.
jest rosnąca.
D. W zbiorze
![]() funkcja
funkcja
![]() jest rosnąca.
jest rosnąca.
E. Funkcja przyjmuje wartość najmniejszą równą 1 dla
![]() .
.
F. Dla
![]() funkcja przyjmuje wartości dodatnie.
funkcja przyjmuje wartości dodatnie.
G. Dla
![]() funkcja przyjmuje wartości dodatnie.
funkcja przyjmuje wartości dodatnie.
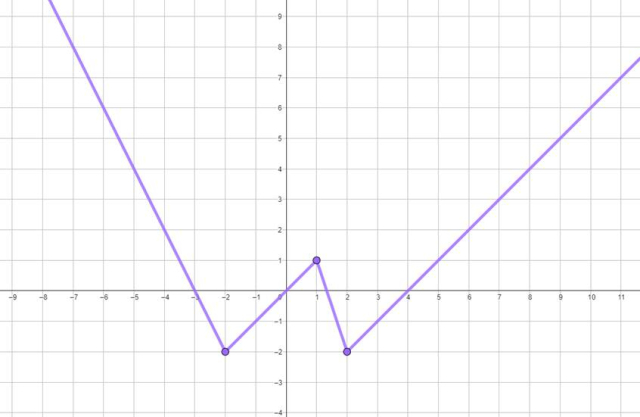
A. Funkcja
![]() przyjmuje wartość najmniejszą równą -2 dla dwóch argumentów:
przyjmuje wartość najmniejszą równą -2 dla dwóch argumentów:
![]() .
.
Zdanie A jest prawdziwe.
B. W przedziale
![]() funkcja
funkcja
![]() jest rosnąca.
jest rosnąca.
Zdanie B jest prawdziwe.
C. W przedziale
![]() funkcja
funkcja
![]() jest rosnąca.
jest rosnąca.
Zdanie C jest prawdziwe.
D. W zbiorze
![]() funkcja
funkcja
![]() jest rosnąca.
jest rosnąca.
Np.:
![]()
![]()
![]()
Zdanie D jest fałszywe.
E. Funkcja przyjmuje wartość największą równą 1 dla
![]() .
.
Zdanie E jest fałszywe.
F. Dla
![]() funkcja przyjmuje wartości dodatnie.
funkcja przyjmuje wartości dodatnie.
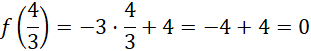
Skoro
![]() na przedziale
na przedziale
![]() jest malejąca i
jest malejąca i
![]() , to dla x mniejszych od
, to dla x mniejszych od
![]() przyjmuje wartości większe od zera.
przyjmuje wartości większe od zera.
Zdanie F jest prawdziwe.
G. Dla
![]() funkcja przyjmuje wartości dodatnie.
funkcja przyjmuje wartości dodatnie.
Zdanie G jest prawdziwe.

Najpierw narysuj podane fragmenty funkcji w odpowiadających im przedziałach. Oznacz miejsce złączenia się prostych kółkiem z wypełnieniem, aby wskazać, że ono również należy do wykresu.
Zdania A-C: skorzystaj ze sporządzonego wykresu.
Zdanie D: skorzystaj z definicji funkcji rosnącej: funkcja
![]() jest rosnąca, jeżeli dla każdych
jest rosnąca, jeżeli dla każdych
![]() i
i
![]() takich, że:
takich, że:
![]() prawdziwa jest zależność, że
prawdziwa jest zależność, że
![]() . W przeciwnym wypadku nie jest rosnąca. Zauważ, że w przedziale
. W przeciwnym wypadku nie jest rosnąca. Zauważ, że w przedziale
![]() jesteś w stanie wyznaczyć takie dwa argumenty x, że dla mniejszego z nich wartość funkcji jest większa, co przeczy definicji funkcji rosnącej.
jesteś w stanie wyznaczyć takie dwa argumenty x, że dla mniejszego z nich wartość funkcji jest większa, co przeczy definicji funkcji rosnącej.
Zdanie E: skorzystaj ze sporządzonego wykresu.
Zdanie F: oblicz najpierw wartość funkcji dla argumentu
![]() . Pamiętaj, aby skorzystać z dobrego wzoru na wartość funkcji dla tego argumentu – wybierz ten wzór, w którego przedziale znajduje się
. Pamiętaj, aby skorzystać z dobrego wzoru na wartość funkcji dla tego argumentu – wybierz ten wzór, w którego przedziale znajduje się
![]() . Wartość funkcji dla argumentu
. Wartość funkcji dla argumentu
![]() jest równa 0. Wiemy również, że jest to funkcja malejąca, więc dla mniejszych argumentów musi przyjmować wartości większe, zatem dla
jest równa 0. Wiemy również, że jest to funkcja malejąca, więc dla mniejszych argumentów musi przyjmować wartości większe, zatem dla
![]() przyjmuje wartości większe od zera.
przyjmuje wartości większe od zera.
Zdanie G: skorzystaj z wiedzy, że zdanie F jest prawdziwe, jak również ze sporządzonego wykresu.

Zadanie 1.4
341Zadanie 1.5
341Zadanie 1.7
341Zadanie 1.8
342Zadanie 1.9
342Zadanie 1.10
342Zadanie 1.11
342Zadanie 1.13
343Zadanie 1.14
343Zadanie 1.15
343Zadanie 1.16
343Zadanie Prosto do matury 4
343Zadanie 2.4
351Zadanie 2.5
351Zadanie 2.6
351Zadanie 2.7
351Zadanie 2.8
351Zadanie 2.9
351Zadanie 2.10
351Zadanie 2.11
352Zadanie 2.16
352Zadanie 2.17
352Zadanie 2.19
352Zadanie 2.21
353Zadanie 2.22
353Zadanie 2.28
353Zadanie 2.29
354Zadanie 2.30
354Zadanie Prosto do matury 3
354Zadanie Prosto do matury 5
354Zadanie 3.4
360Zadanie 3.5
360Zadanie 3.6
360Zadanie 3.7
360Zadanie 3.9
361Zadanie 3.10
361Zadanie 3.11
361Zadanie 3.14
361Zadanie 3.16
362Zadanie 4.4
366Zadanie 4.5
367Zadanie 4.6
367Zadanie 4.7
367Zadanie 4.8
367Zadanie 4.9
367Zadanie 4.10
368Zadanie 4.12
369Zadanie 4.13
369Zadanie 5.5
377Zadanie 5.6
377Zadanie 5.7
377Zadanie 5.8
377Zadanie 5.9
377Zadanie 5.11
377Zadanie 5.12
378Zadanie 5.13
378Zadanie 5.14
378Zadanie 5.16
378Zadanie 5.17
378Zadanie 5.18
378Zadanie 5.19
378Zadanie 5.20
378Zadanie 5.21
379Zadanie 5.22
379Zadanie 6.6
384Zadanie 6.8
384Zadanie 6.9
384Zadanie 7.5
390Zadanie 7.6
391Zadanie 7.7
391Zadanie 7.8
391Zadanie 7.12
392Zadanie 8.32
397Zadanie 8.36
397Zadanie 8.37
397Zadanie 8.38
397Zadanie 8.39
398Zadanie 8.40
398Zadanie 8.41
398Zadanie 8.48
398Zadanie 8.49
399Zadanie 8.56
400Zadanie 8.57
400Zadanie 8.58
400
