Liczby: 3, b, c tworzą w podanej kolejności rosnący ciąg geometryczny. Wiedząc, iż te liczby są w podanej kolejności pierwszym, drugim i piątym wyrazem ciągu arytmetycznego, podaj wartości b i c.
Jeśli liczby tworzą ciąg geometryczny, to spełniają warunek:
![]()
Własność ciągu arytmetycznego:
Drugi wyraz to b:
![]() , gdzie r to różnica tego ciągu
, gdzie r to różnica tego ciągu
![]()
Wynika z tego, że
![]()
![]()
![]()
![]()
Wstaw do równania z ciągiem geometrycznym:
![]()
![]()
![]()
![]()
![]()
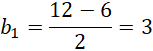
Rozwiązanie c:
![]()
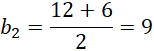
![]()
Ciąg geometryczny w pierwszym przypadku:
![]() – nie jest to ciąg rosnący – rozwiązanie odrzuć
– nie jest to ciąg rosnący – rozwiązanie odrzuć
W drugim przypadku:
![]() – jest to ciąg rosnący, jedyna poprawna odpowiedź.
– jest to ciąg rosnący, jedyna poprawna odpowiedź.
Odpowiedź b = 9, c = 27.

Pewien wyraz ciągu geometrycznego podniesiony do kwadratu jest równy iloczynowi poprzedniego i następnego wyrazu ciągu.
Wzór na n-ty wyraz ciągu arytmetycznego:
![]() ,
,
Gdzie a1 – pierwszy wyraz ciągu arytmetycznego,
n – liczba wyrazów ciągu,
r – różnica ciągu (o ile zwiększa się lub zmniejsza każdy kolejny wyraz ciągu arytmetycznego, w porównaniu do poprzedniego wyrazu).

Zadanie 33
128Zadanie 31
133Zadanie 34
146Zadanie 27
150Zadanie 27
154Zadanie 27
162Zadanie 29
166
