Wiedząc, że punkt
![]() należy do okręgu, który jest styczny do osi
należy do okręgu, który jest styczny do osi
![]() w punkcie
w punkcie
![]() , podaj różnicę pomiędzy polem kwadratu wpisanego w ten okrąg a polem trójkąta równobocznego, również wpisanego w tenże okrąg.
, podaj różnicę pomiędzy polem kwadratu wpisanego w ten okrąg a polem trójkąta równobocznego, również wpisanego w tenże okrąg.
Kiedy wpiszemy kwadrat w okrąg:
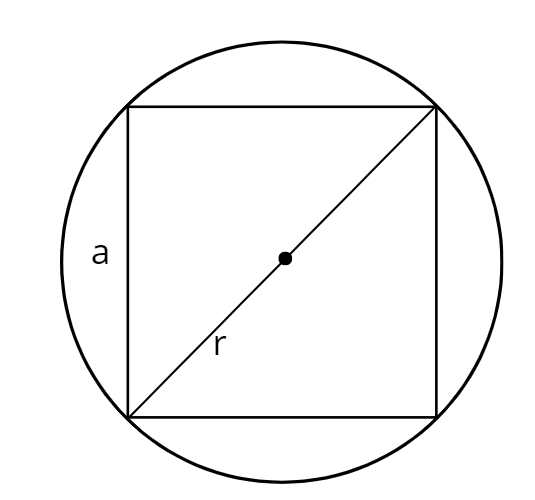
Przekątna kwadratu:
![]()
Pole kwadratu:
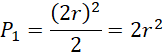
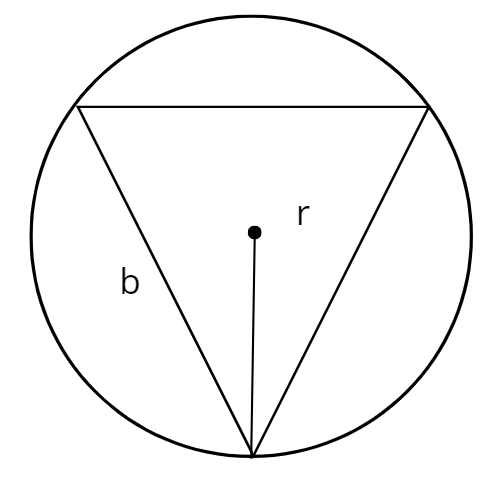
Promień to:
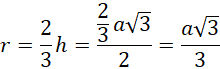
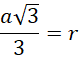
![]()
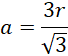
Pole tego trójkąta:
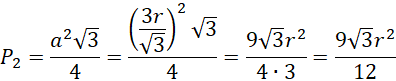
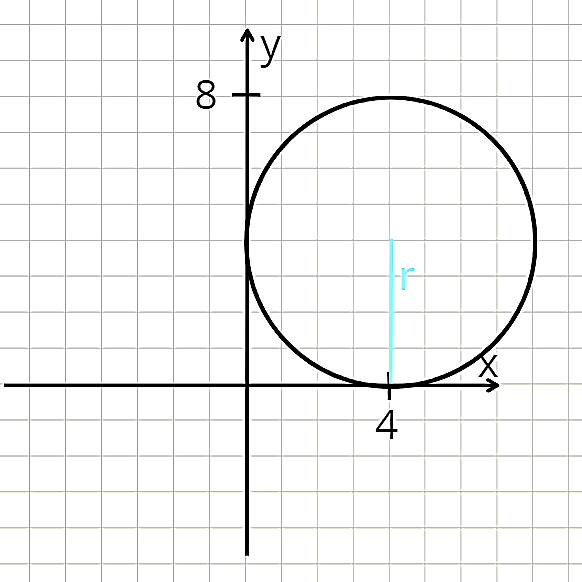
Widzimy, że r może być równe tylko 4, gdyż inaczej punkt (4,8) nie należałby do okręgu.
Różnica pól:
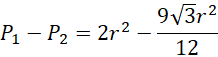
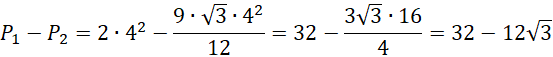

Styczny do okręgu oznacza prostopadły do promienia. Promień musi być prostopadły do osi OX.
Przekątna kwadratu wpisanego w okrąg jest równa średnicy tego okręgu.
Wzór na pole kwadratu, znając jego przekątną d ma postać:
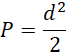
W trójkącie równobocznym wpisanym w okrąg promień jest równy dwum trzecim wysokości tego trójkąta.
Wzór na wysokość w trójkącie równobocznym o boku a:
![]() .
.
Pole trójkąta równobocznego:
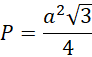

Zadanie 33
128Zadanie 31
133Zadanie 34
146Zadanie 27
150Zadanie 27
154Zadanie 27
162Zadanie 29
166
