W tym zadaniu musisz wyznaczyć równanie prostej k, która jest równoległa do prostej l, na dwa sposoby.
1 sposób: skorzystaj z twierdzenia 1, czyli
ABl–AlB = 0, gdzie Ak, Bk–współczynniki prostej l; A,B–współczynniki prostej k
ABl = AlB ,
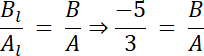
Prosta l: Ax + By + C = 0, gdzie punkt (0,0) należy do tej prostej:
A∙0 + B∙0 + C = 0, więc C = 0
prosta l: Ax + By = 0
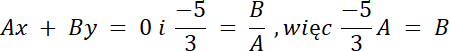
![]()
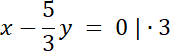
prosta k: 3x–5y = 0
2 sposób:
prosta l: 3x–5y + 1 = 0 | + 5y
3x + 1 = 5y | /5
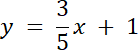
warunek równoległości prostych kierunkowych: ak = al
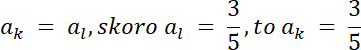
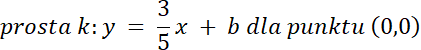
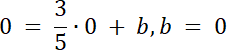
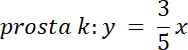

Wyznacz równanie prostej k, dwoma metodami–rozwiąż zadania na podstawie schematu z podręcznika.

Zadanie 2.
192Zadanie 4.
192Zadanie 5.
192Zadanie 6.
192Zadanie 1.
198Zadanie 2.
198Zadanie 3.
198Zadanie 4.
198Zadanie 5.
198Zadanie 6.
198Zadanie 7.
198Zadanie 8.
198Zadanie 2.
204Zadanie 3.
204Zadanie 4.
204Zadanie 5.
204Zadanie 6.
204Zadanie 7.
204Zadanie 1.
208Zadanie 2.
208Zadanie 3.
208Zadanie 4.
208Zadanie 5.
208Zadanie 6.
208Zadanie 7.
208Zadanie 1.
213Zadanie 2.
213Zadanie 3.
213Zadanie 4.
213Zadanie 3.
216Zadanie 7.
218Zadanie 13.
218Zadanie 14.
218Zadanie 16.
218Zadanie 20.
218
