W tym zadaniu musisz wyznaczyć współrzędne punktu C, który znajduje się na osi odciętych.
Punkt C (x, 0)–znajduje się na osi odciętych
AC jest prostopadła do BC, więc:
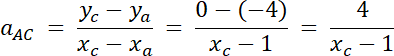
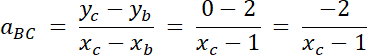
8 = (xc–1)2 | /√
2√2 = xc–1 v–2√2 = xc–1 | + 1
xc = 2√2 + 1 v xc = –2√2 + 1, czyli
C(–2√2 + 1, 0) v C(2√2 + 1, 0)

Na początku zauważ, że skoro punkt C ma znaleźć się na osi odciętych to: C(x,0). Dodatkowo trójkąt ma być prostokątny, więc proste AC i BC są do siebie prostopadłe–skorzystaj z warunku na proste prostopadłe–który uwzględnia współczynniki kierunkowe i wyznacz współrzędną x punktu C.

Zadanie 2.
192Zadanie 4.
192Zadanie 5.
192Zadanie 6.
192Zadanie 1.
198Zadanie 2.
198Zadanie 3.
198Zadanie 4.
198Zadanie 5.
198Zadanie 6.
198Zadanie 7.
198Zadanie 8.
198Zadanie 2.
204Zadanie 3.
204Zadanie 4.
204Zadanie 5.
204Zadanie 6.
204Zadanie 7.
204Zadanie 1.
208Zadanie 2.
208Zadanie 3.
208Zadanie 4.
208Zadanie 5.
208Zadanie 6.
208Zadanie 7.
208Zadanie 1.
213Zadanie 2.
213Zadanie 3.
213Zadanie 4.
213Zadanie 3.
216Zadanie 7.
218Zadanie 13.
218Zadanie 14.
218Zadanie 16.
218Zadanie 20.
218
