W tym zadaniu, na podstawie współrzędnych trójkąta ABC, wyznacz równanie prostej CS.
Wyznacz środek odcinka AB:
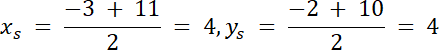
S(4, 4) i C(0, 7), więc: prosta CS: y = ax + b
7 = a∙0 + b⇒ b = 7,
4 = a∙4 + 7 |–7
–3 = 4a | /4
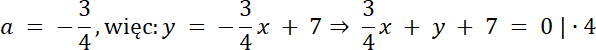
Równanie prostej CS:
![]()

Środkowa CS wychodzi z punktu C i przecina odcinek AB, w punkcie środkowym, więc najpierw wyznacz środek odcinka AB, a następnie na podstawie współrzędnych punktu C i S wyznacz prostą, na której znajdują się punkty C i S.

Zadanie 2.
192Zadanie 4.
192Zadanie 5.
192Zadanie 6.
192Zadanie 1.
198Zadanie 2.
198Zadanie 3.
198Zadanie 4.
198Zadanie 5.
198Zadanie 6.
198Zadanie 7.
198Zadanie 8.
198Zadanie 2.
204Zadanie 3.
204Zadanie 4.
204Zadanie 5.
204Zadanie 6.
204Zadanie 7.
204Zadanie 1.
208Zadanie 2.
208Zadanie 3.
208Zadanie 4.
208Zadanie 5.
208Zadanie 6.
208Zadanie 7.
208Zadanie 1.
213Zadanie 2.
213Zadanie 3.
213Zadanie 4.
213Zadanie 3.
216Zadanie 7.
218Zadanie 13.
218Zadanie 14.
218Zadanie 16.
218Zadanie 20.
218
