W tym zadaniu musisz wyznaczyć współrzędne punktów A, B, C.
Wierzchołek paraboli: W(–3, 0),⇒ C(–3, 0),
A(–x–3, yA), B(x–3, yB)⇒ yA = yB = y
Odcinek |AB|–przeciwprostokątna trójkąta ABC:
AC jest prostopadłe do BC–aAC∙aBC = –1,:
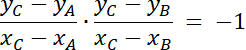
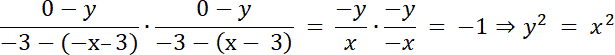
y = x, bo x > 0, więc:
A(–x–3, x), B(x–3, x) = A(–y–3, y), B(y–3, y);
y = 0,25(y–3 + 3)2
y = 0,25y2 |∙4
4y = y2 |–4y
y2–4y = 0
y(y–4) = 0
y = 0 v y = 4, y > 0, więc y = 4:
B: x = y–3 = 4–3 = 1
A: x = –y–3 = –4–3 = –7
Współrzędne punktów: A(–7, 4), B(1, 4), C(–3, 0)

W pierwszym kroku–z równania kanonicznego paraboli–wyznacz współrzędne wierzchołka. Zauważ, że wierzchołek W to punkt C(–3, 0) trójkąta, ponieważ bok AB jest równoległy do osi OX, więc yA = yB. Na tej podstawie wyznacz zależność na współrzędną x punktu A i B. Wyznacz zależność na współrzędną y dla punktów A i B, korzystając z informacji, że proste AC i BC są prostopadłe. Na koniec skorzystaj z równania paraboli, aby wyznaczyć wartość y–pamiętaj, że dla punktów A i B, y > 0–punkty znajdują się na paraboli, a wierzchołek paraboli jest w punkcie (–3, 0).

Zadanie 2.
192Zadanie 4.
192Zadanie 5.
192Zadanie 6.
192Zadanie 1.
198Zadanie 2.
198Zadanie 3.
198Zadanie 4.
198Zadanie 5.
198Zadanie 6.
198Zadanie 7.
198Zadanie 8.
198Zadanie 2.
204Zadanie 3.
204Zadanie 4.
204Zadanie 5.
204Zadanie 6.
204Zadanie 7.
204Zadanie 1.
208Zadanie 2.
208Zadanie 3.
208Zadanie 4.
208Zadanie 5.
208Zadanie 6.
208Zadanie 7.
208Zadanie 1.
213Zadanie 2.
213Zadanie 3.
213Zadanie 4.
213Zadanie 3.
216Zadanie 7.
218Zadanie 13.
218Zadanie 14.
218Zadanie 16.
218Zadanie 20.
218
