W tym zadaniu musisz udowodnić, że punkt wspólny prostej k i l należy do okręgu.
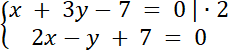
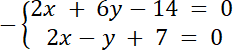
7y–21 = 0 | + 21
7y = 21 | /7
y = 3⇒ 2x–3 + 7 = 0⇒ 2x + 4 = 0 |–4⇒ 2x = –4 | /2⇒ x = –2
punkt wspólny prostej k i l: (–2, 3)
dane okręgu: S(1, 2), r = √10
równanie okręgu: (x–1)2 + (y–2)2 = 10 dla (–2, 3)
(–2–1)2 + (3–2)2 = 32 + 12 = 9 + 1 = 10
10 = 10–punkt przecięcia prostych k i l należy do okręgu.

W pierwszym kroku wyznacz punkt przecięcia prostych k i l, a następnie na podstawie współrzędnych środka okręgu i promienia, napisz równanie kanoniczne okręgu. Na koniec udowodnij, że punkt przecięcia prostych należy do okręgu–czy lewa strona równania okręgu jest równa prawej.

Zadanie 2.
192Zadanie 4.
192Zadanie 5.
192Zadanie 6.
192Zadanie 1.
198Zadanie 2.
198Zadanie 3.
198Zadanie 4.
198Zadanie 5.
198Zadanie 6.
198Zadanie 7.
198Zadanie 8.
198Zadanie 2.
204Zadanie 3.
204Zadanie 4.
204Zadanie 5.
204Zadanie 6.
204Zadanie 7.
204Zadanie 1.
208Zadanie 2.
208Zadanie 3.
208Zadanie 4.
208Zadanie 5.
208Zadanie 6.
208Zadanie 7.
208Zadanie 1.
213Zadanie 2.
213Zadanie 3.
213Zadanie 4.
213Zadanie 3.
216Zadanie 7.
218Zadanie 13.
218Zadanie 14.
218Zadanie 16.
218Zadanie 20.
218
