W tym zadaniu skorzystaj ze wzorów na współrzędne środka odcinka i na współrzędne środka ciężkości, aby obliczyć szukane wartości tego zadania.
![]()
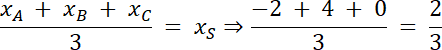
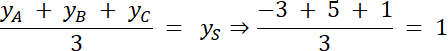
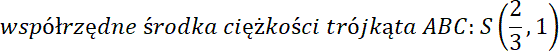
Środek ciężkości trójkąta–punkt przecięcia środkowych trójkąta,
Poniżej, rysunek poglądowy:
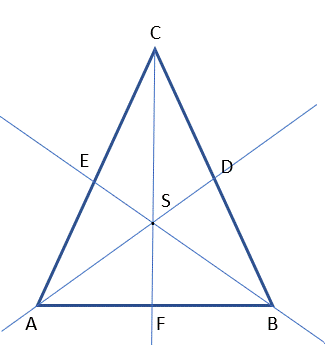
|SD| : |AS| = 1 : 2⇒ 2|SD| = |AS|
|AD| = |AS| + |SD|
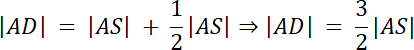
![]()
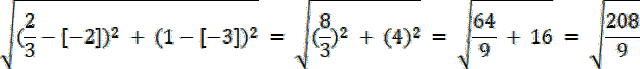
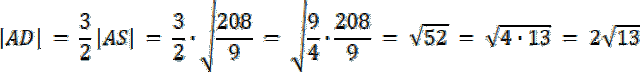
|SE| : |BS| = 1 : 2⇒ 2|SE| = |BS|
|BE| = |BS| + |SE|
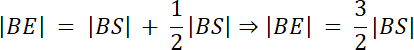
![]()
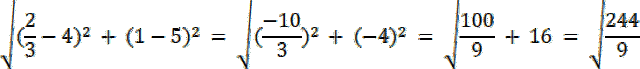
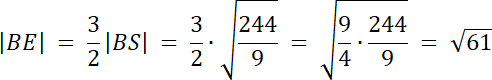
|SF| : |CS| = 1 : 2⇒ 2|SF| = |CS|
|CF| = |CS| + |SF|

![]()
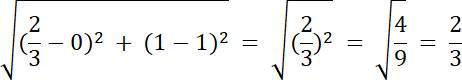
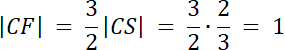

W tym zadaniu musisz skorzystać ze wzoru na środek ciężkości trójkąta (punkt S). Dodatkowo środek ciężkości dzieli każdą środkową trójkąta w stosunku 1:2, więc
|CS| = 2|SF| oraz |CD| = |CS| + |SD|, a stąd |CD| = 3|SD|. Przeprowadź to działanie dla każdego boku trójkąta i wyznacz długości środkowych.

Zadanie 2.
192Zadanie 4.
192Zadanie 5.
192Zadanie 6.
192Zadanie 1.
198Zadanie 2.
198Zadanie 3.
198Zadanie 4.
198Zadanie 5.
198Zadanie 6.
198Zadanie 7.
198Zadanie 8.
198Zadanie 2.
204Zadanie 3.
204Zadanie 4.
204Zadanie 5.
204Zadanie 6.
204Zadanie 7.
204Zadanie 1.
208Zadanie 2.
208Zadanie 3.
208Zadanie 4.
208Zadanie 5.
208Zadanie 6.
208Zadanie 7.
208Zadanie 1.
213Zadanie 2.
213Zadanie 3.
213Zadanie 4.
213Zadanie 3.
216Zadanie 7.
218Zadanie 13.
218Zadanie 14.
218Zadanie 16.
218Zadanie 20.
218
