W tym zadaniu, na podstawie rysunku, musisz wypisać dane dla prostej l i paraboli p i wyznaczyć ich równania, a następnie znajdź punkty wspólne tych krzywych.
parabola p: a(x + 6)(x–2), gdzie punkt (0,–3) należy do tej paraboli, więc:
a(0 + 6)(0–2) = –3
a(6)(–2) = –3⇒–12a = –3 | /(–12)
a = 0,25, więc równanie paraboli p: 0,25(x + 6)(x–2)
prosta l, punkty należące do niej: (–7, 0), (0,–7)
y = ax + b–równanie kierunkowe prostej l:
–7 = a∙0 + b⇒ b = –7
0 = –7∙a–7 | + 7
7 = –7a | /(–7)
a = –1, więc równanie kierunkowe proste l: y = –x–7⇒ x + y + 7 = 0
Część wspólna:
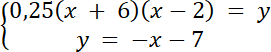
0,25(x + 6)(x–2) = –x–7
0,25(x2 + 4x–12) = –x–7
0,25x2 + x–3 = –x–7 | + x + 7
0,25x2 + 2x + 4 = 0 |∙4
x2 + 8x + 16 = 0
(x + 4)2 = 0
x = –4, y = –(–4)–7 = –3
Punkt wspólny krzywych: (–4,–3)

Z rysunku możesz wyczytać: współrzędne dwóch punktów, które należą do prostej l–dzięki czemu jesteś w stanie wyznaczyć równanie kierunkowe tej prostej. Na podstawie dwóch miejsc zerowych paraboli oraz punktu (0,–3) możesz wyznaczyć równanie paraboli w postaci iloczynowej, a na koniec przyrównaj równania dwóch krzywych, aby wyznaczyć punkt wspólny.

Zadanie 2.
192Zadanie 4.
192Zadanie 5.
192Zadanie 6.
192Zadanie 1.
198Zadanie 2.
198Zadanie 3.
198Zadanie 4.
198Zadanie 5.
198Zadanie 6.
198Zadanie 7.
198Zadanie 8.
198Zadanie 2.
204Zadanie 3.
204Zadanie 4.
204Zadanie 5.
204Zadanie 6.
204Zadanie 7.
204Zadanie 1.
208Zadanie 2.
208Zadanie 3.
208Zadanie 4.
208Zadanie 5.
208Zadanie 6.
208Zadanie 7.
208Zadanie 1.
213Zadanie 2.
213Zadanie 3.
213Zadanie 4.
213Zadanie 3.
216Zadanie 7.
218Zadanie 13.
218Zadanie 14.
218Zadanie 16.
218Zadanie 20.
218
