W tym zadaniu musisz wyznaczyć współrzędne punktu C.
prosta AC: y = ax + b, gdzie:
tg α = 2 i tg α = a⇒ a = 2
–2 = 2∙(–3) + b⇒–2 = –6 + b | + 6⇒ b = 4, więc
prosta AC: y = 2x + 4; C(x, 2x + 4)
![]()
Odcinek |AB|–przeciwprostokątna trójkąta, więc:
|BC|2 + |AC|2 = |AB|2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5x2 + 14x + 61 + 5x2 + 30x + 45 = 64 |–64
10x2 + 44x + 42 = 0 | /10
x2 + 4,4x + 2,2 = 0
∆ = (4,4)2–4∙4,2 = 19,36–16,8 = 2,56
√∆ = √2,56 = 1,6
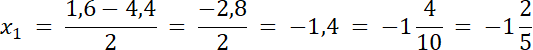
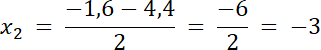
![]()
dla x = –3, y = 2∙(–3) + 4 = –2⇒ (–3,–2)–współrzędne punktu A, więc
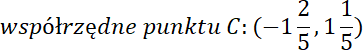

W pierwszym kroku wyznacz równanie prostej AC, aby wyznaczyć zależność na współrzędne dla punktu C. Następnie z twierdzenia Pitagorasa, zapisz stosunek długości boków trójkąta ABC: |BC|2 + |AC|2 = |AB|2–przeciwprostokątna trójkąta ABC–bok |AB| bo |∢ACB| = 90° i wyznacz z tego równania współrzędne punktu C.

Zadanie 2.
192Zadanie 4.
192Zadanie 5.
192Zadanie 6.
192Zadanie 1.
198Zadanie 2.
198Zadanie 3.
198Zadanie 4.
198Zadanie 5.
198Zadanie 6.
198Zadanie 7.
198Zadanie 8.
198Zadanie 2.
204Zadanie 3.
204Zadanie 4.
204Zadanie 5.
204Zadanie 6.
204Zadanie 7.
204Zadanie 1.
208Zadanie 2.
208Zadanie 3.
208Zadanie 4.
208Zadanie 5.
208Zadanie 6.
208Zadanie 7.
208Zadanie 1.
213Zadanie 2.
213Zadanie 3.
213Zadanie 4.
213Zadanie 3.
216Zadanie 7.
218Zadanie 13.
218Zadanie 14.
218Zadanie 16.
218Zadanie 20.
218
