W tym zadaniu musisz wyznaczyć współrzędne punktów, w których proste k i l przecinają osie OX i OY.
prosta k: tg 60° = a; tg 60° = √3, więc ak = √3
punkt P(√3, 3) należy do prostej k, więc:
3 = √3∙√3 + b⇒ 3 = 3 + b |–3⇒ b = 0
prosta k: y = √3x
prosta l: ak∙al = –1⇒ √3∙al = –1 | /√3
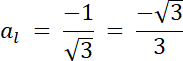
![]()
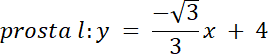
prosta k: x = 0,⇒ y = √3∙0⇒ y = 0
prosta l: dla
![]()
dla
![]()
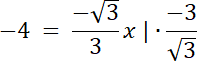
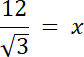
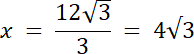
prosta k: (0, 0)–punkt przecięcia z osią OX i OY
prosta l: (0, 4)–punkt przecięcia z osią OY, (4√3, 0)–punkt przecięcia z osią OX

W pierwszym kroku wyznacz równanie kierunkowe prostej k, następnie prostej l, a na koniec oblicz punkty, w którym prosta k i prosta l przecinają osie: OX i OY.

Zadanie 2.
192Zadanie 4.
192Zadanie 5.
192Zadanie 6.
192Zadanie 1.
198Zadanie 2.
198Zadanie 3.
198Zadanie 4.
198Zadanie 5.
198Zadanie 6.
198Zadanie 7.
198Zadanie 8.
198Zadanie 2.
204Zadanie 3.
204Zadanie 4.
204Zadanie 5.
204Zadanie 6.
204Zadanie 7.
204Zadanie 1.
208Zadanie 2.
208Zadanie 3.
208Zadanie 4.
208Zadanie 5.
208Zadanie 6.
208Zadanie 7.
208Zadanie 1.
213Zadanie 2.
213Zadanie 3.
213Zadanie 4.
213Zadanie 3.
216Zadanie 7.
218Zadanie 13.
218Zadanie 14.
218Zadanie 16.
218Zadanie 20.
218
