Wskaż prawidłowe zdania dla układu równań 
A. Dla b = 1 i c = 5 układ spełnia nieskończenie wiele par liczb.
B. Dla b = 1 i c ≠ 5 układ nie ma rozwiązań.
C. Dla b = -1 i c = 5 rozwiązaniem układu równań jest para liczb 
A. 
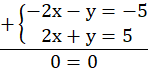
Układ jest nieoznaczony, więc zdanie jest prawdziwe.
B. Zdanie jest prawdziwe, ponieważ jeśli c jest różne od 5 to niewiadome x oraz y się redukują.
C.
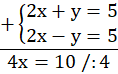
Zdanie jest prawdziwe.
A. Dla b= 1 i c = 5 układ spełnia nieskończenie wiele par liczb.
B. Dla b = 1 i c ≠ 5 układ nie ma rozwiązań.
C. Dla b = -1 i c = 5 rozwiązaniem układu równań jest para liczb 
Sprawdź, czy zdanie A jest prawdziwe poprzez podstawienie b = 1 oraz c = 5 do równania. Pomnóż pierwsze równanie przez (-1), aby otrzymać przy niewiadomej x liczby przeciwne, a następnie dodaj do siebie równania.
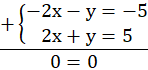
Wszystkie niewiadome oraz wiadome się redukują, co oznacza, że układ równań jest nieoznaczony, ponieważ układ równań ma nieskończenie wiele rozwiązań.
Zdanie B prawdziwe, ponieważ jeśli c jest różne od 5 to niewiadome x oraz y się redukują i zostanie tylko wolna liczba.
Sprawdź, czy zdanie C jest prawdziwe poprzez podstawienie b = -1 oraz c = 5 do równania, a następnie dodaj do siebie równania.
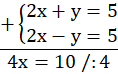
Dzięki temu wyliczysz jedną niewiadomą, którą następnie podstaw do jednego z równań i wylicz drugą niewiadomą.
