W zadaniu musisz udowodnić, że funkcja g określona wzorem
![]() jest funkcją parzystą.
jest funkcją parzystą.
Założenia:
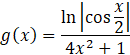
Teza:
Jeśli
![]() , to
, to
![]() oraz
oraz
![]()
Dowód:
Dziedzina:
![]()
![]()
![]()
![]()
Dla każdego x należącego do dziedziny funkcji -x także należy do dziedziny.
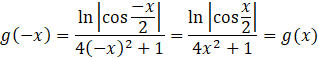
Dla
![]() oraz
oraz
![]() , zatem funkcja jest parzysta, co należało wykazać.
, zatem funkcja jest parzysta, co należało wykazać.

Funkcja g jest funkcją logarytmiczną, czyli ma postać:
![]() gdzie
gdzie
![]()
Aby zatem wyznaczyć dziedzinę funkcji, musisz obliczyć, dla jakich argumentów:
![]()
Wartość bezwzględna z dowolnej liczby rzeczywistej jest zawsze większa bądź równa 0, a więc musisz obliczyć argumenty, dla których:
![]()
Nierówność
![]() jest spełniona dla każdej rzeczywistej liczby x, zatem pozostaje obliczyć, dla jakich argumentów:
jest spełniona dla każdej rzeczywistej liczby x, zatem pozostaje obliczyć, dla jakich argumentów:
![]()
![]()
Czyli:
![]()
Zatem:
![]()
Funkcja f jest parzysta, gdy dla każdego x należącego do dziedziny funkcji, -x także należy do dziedziny oraz
![]() .
.
W zadaniu musisz także wiedzieć, że funkcja
![]() jest parzysta, zatem:
jest parzysta, zatem:
![]()

Ćwiczenie 1.
57Zadanie 1.
61Zadanie 2.
61Zadanie 3.
61Zadanie 4.
61Zadanie 5.
61Zadanie 6.
61Zadanie 7.
62Zadanie 9.
62Zadanie 16.
62Ćwiczenie 1.
64Zadanie 1.
68Zadanie 2.
68Zadanie 5.
69Zadanie 6.
69Zadanie 7.
69Zadanie 8.
69Zadanie 9.
69Zadanie 11.
69Zadanie 12.
69Zadanie 13.
70Zadanie 24.
70Zadanie 1.
77Zadanie 2.
77Zadanie 3.
77Zadanie 4.
77Zadanie 5.
77Zadanie 6.
77Zadanie 7.
77Zadanie 9.
78Zadanie 10.
78Zadanie 11.
78Zadanie 12.
78Zadanie 13.
78Zadanie 14.
78Zadanie 15.
78Zadanie 16.
78Zadanie 1.
83Zadanie 2.
84Zadanie 3.
84Zadanie 4.
84Zadanie 5.
84Zadanie 6.
84Zadanie 7.
84Zadanie 8.
85Zadanie 9.
85Zadanie 12.
85Zadanie 13.
85Zadanie 1.
91Zadanie 2.
92Zadanie 3.
92Zadanie 4.
92Zadanie 5.
92Zadanie 6.
92Zadanie 10.
92Zadanie 1.
98Zadanie 2.
99Zadanie 5.
99Zadanie 6.
99Zadanie 8.
99Zadanie 11.
101Zadanie 18.
101Zadanie 19.
101Zadanie 20.
102Zadanie 21.
102Zadanie 22.
102Zadanie 26.
102Zadanie 27.
102Zadanie 28.
103Zadanie 29.
103Zadanie 32.
103Zadanie 33.
103Zadanie 34.
103Zadanie 36.
103
