W zadaniu musisz udowodnić, że funkcja f określona wzorem
![]() w przedziale
w przedziale
![]() przyjmuje największą wartość równą -2.
przyjmuje największą wartość równą -2.
Założenia:
![]()
Teza:
Funkcja f w przedziale
![]() przyjmuje największą wartość równą -2.
przyjmuje największą wartość równą -2.
Dowód:
Dziedzina funkcji f:
![]()
![]()
![]() oraz współczynnik przy
oraz współczynnik przy
![]() jest większy od 0, a więc parabola ma ramiona skierowane w górę. Dziedziną funkcji f jest zatem zbiór liczb rzeczywistych. Zbiór
jest większy od 0, a więc parabola ma ramiona skierowane w górę. Dziedziną funkcji f jest zatem zbiór liczb rzeczywistych. Zbiór
![]() zawiera się w dziedzinie funkcji.
zawiera się w dziedzinie funkcji.
Funkcja f jest funkcją złożoną ciągłą:
![]() , gdzie:
, gdzie:
![]()
![]()
Zbiór wartości funkcji g:
![]()
![]()
![]()
![]()
![]()
Dziedziną funkcji h jest zatem
![]() . Podstawa logarytmu
. Podstawa logarytmu
![]() , zatem funkcja h jest funkcją malejącą. Oznacza to, że w przedziale
, zatem funkcja h jest funkcją malejącą. Oznacza to, że w przedziale
![]() największą wartość przyjmie dla
największą wartość przyjmie dla
![]() , równą:
, równą:
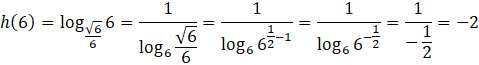
Największa wartość funkcji h w przedziale
![]() to równocześnie największa wartość funkcji f w przedziale
to równocześnie największa wartość funkcji f w przedziale
![]() . Funkcja f w przedziale
. Funkcja f w przedziale
![]() przyjmuje zatem największą wartość równą -2, co należało wykazać.
przyjmuje zatem największą wartość równą -2, co należało wykazać.

Funkcja f jest funkcją ciągłą, złożoną z dwóch funkcji ciągłych: funkcji wewnętrznej
![]() , gdzie
, gdzie
![]() , oraz zewnętrznej
, oraz zewnętrznej
![]() , której dziedziną jest zbiór wartości funkcji g. Zbiór wartości funkcji f jest natomiast taki sam jak zbiór wartości funkcji zewnętrznej h. Aby zatem znaleźć największą wartość funkcji f, musisz wyznaczyć największą wartość funkcji
, której dziedziną jest zbiór wartości funkcji g. Zbiór wartości funkcji f jest natomiast taki sam jak zbiór wartości funkcji zewnętrznej h. Aby zatem znaleźć największą wartość funkcji f, musisz wyznaczyć największą wartość funkcji
![]() .
.
Zacznij od wyznaczenia zbioru wartości funkcji g. Wykres funkcji g jest parabolą o ramionach skierowanych w górze. Musisz zatem zacząć od sprawdzenia, czy pierwsza współrzędna wierzchołka funkcji należy do przedziału
![]() , a następnie obliczyć wartość funkcji w wierzchołku dla znalezionego argumentu. Wartość największą funkcja osiągnie na końcach przedziału, czyli dla argumentu
, a następnie obliczyć wartość funkcji w wierzchołku dla znalezionego argumentu. Wartość największą funkcja osiągnie na końcach przedziału, czyli dla argumentu
![]() lub dla argumentu
lub dla argumentu
![]() .
.
Największą wartość funkcji h oblicz korzystając z własności działań na logarytmach.

Ćwiczenie 1.
57Zadanie 1.
61Zadanie 2.
61Zadanie 3.
61Zadanie 4.
61Zadanie 5.
61Zadanie 6.
61Zadanie 7.
62Zadanie 9.
62Zadanie 16.
62Ćwiczenie 1.
64Zadanie 1.
68Zadanie 2.
68Zadanie 5.
69Zadanie 6.
69Zadanie 7.
69Zadanie 8.
69Zadanie 9.
69Zadanie 11.
69Zadanie 12.
69Zadanie 13.
70Zadanie 24.
70Zadanie 1.
77Zadanie 2.
77Zadanie 3.
77Zadanie 4.
77Zadanie 5.
77Zadanie 6.
77Zadanie 7.
77Zadanie 9.
78Zadanie 10.
78Zadanie 11.
78Zadanie 12.
78Zadanie 13.
78Zadanie 14.
78Zadanie 15.
78Zadanie 16.
78Zadanie 1.
83Zadanie 2.
84Zadanie 3.
84Zadanie 4.
84Zadanie 5.
84Zadanie 6.
84Zadanie 7.
84Zadanie 8.
85Zadanie 9.
85Zadanie 12.
85Zadanie 13.
85Zadanie 1.
91Zadanie 2.
92Zadanie 3.
92Zadanie 4.
92Zadanie 5.
92Zadanie 6.
92Zadanie 10.
92Zadanie 1.
98Zadanie 2.
99Zadanie 5.
99Zadanie 6.
99Zadanie 8.
99Zadanie 11.
101Zadanie 18.
101Zadanie 19.
101Zadanie 20.
102Zadanie 21.
102Zadanie 22.
102Zadanie 26.
102Zadanie 27.
102Zadanie 28.
103Zadanie 29.
103Zadanie 32.
103Zadanie 33.
103Zadanie 34.
103Zadanie 36.
103
