W zadaniu musisz wyznaczyć wartości liczb a i b, występujące we wzorze funkcji
![]() , gdzie
, gdzie
![]() , wiedząc, że do wykresu funkcji f należą punkty
, wiedząc, że do wykresu funkcji f należą punkty
![]() i
i
![]() , a następnie obliczyć miejsce zerowe funkcji.
, a następnie obliczyć miejsce zerowe funkcji.
![]()
![]()
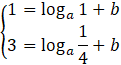
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() nie należy do dziedziny, zatem jedynym prawidłowym rozwiązaniem jest
nie należy do dziedziny, zatem jedynym prawidłowym rozwiązaniem jest
![]() .
.
![]()
![]()
![]()
![]()
![]() – miejsce zerowe
– miejsce zerowe

Szukana funkcja ma postać:
![]() , gdzie
, gdzie
![]()
Do wykresu funkcji należy punkt
![]() , czyli:
, czyli:
![]()
oraz punkt
![]() , czyli:
, czyli:
![]()
Aby wyznaczyć wzór funkcji, musisz rozwiązać układ równań:
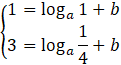
gdzie
![]()
Z pierwszego równania otrzymujesz:
![]()
![]()
Wstaw znalezione b do drugiego równania:
![]()
![]()
![]()
Z definicji logarytmu:
![]()
Zatem:
![]()
![]() nie należy do dziedziny, zatem jedynym prawidłowym rozwiązaniem jest
nie należy do dziedziny, zatem jedynym prawidłowym rozwiązaniem jest
![]() .
.
Wzór funkcji f wygląda zatem następująco:
![]()
Znajdź miejsce zerowe funkcji:
![]()
![]()
Z definicji logarytmu:
![]()
![]()

Ćwiczenie 1.
57Zadanie 1.
61Zadanie 2.
61Zadanie 3.
61Zadanie 4.
61Zadanie 5.
61Zadanie 6.
61Zadanie 7.
62Zadanie 9.
62Zadanie 16.
62Ćwiczenie 1.
64Zadanie 1.
68Zadanie 2.
68Zadanie 5.
69Zadanie 6.
69Zadanie 7.
69Zadanie 8.
69Zadanie 9.
69Zadanie 11.
69Zadanie 12.
69Zadanie 13.
70Zadanie 24.
70Zadanie 1.
77Zadanie 2.
77Zadanie 3.
77Zadanie 4.
77Zadanie 5.
77Zadanie 6.
77Zadanie 7.
77Zadanie 9.
78Zadanie 10.
78Zadanie 11.
78Zadanie 12.
78Zadanie 13.
78Zadanie 14.
78Zadanie 15.
78Zadanie 16.
78Zadanie 1.
83Zadanie 2.
84Zadanie 3.
84Zadanie 4.
84Zadanie 5.
84Zadanie 6.
84Zadanie 7.
84Zadanie 8.
85Zadanie 9.
85Zadanie 12.
85Zadanie 13.
85Zadanie 1.
91Zadanie 2.
92Zadanie 3.
92Zadanie 4.
92Zadanie 5.
92Zadanie 6.
92Zadanie 10.
92Zadanie 1.
98Zadanie 2.
99Zadanie 5.
99Zadanie 6.
99Zadanie 8.
99Zadanie 11.
101Zadanie 18.
101Zadanie 19.
101Zadanie 20.
102Zadanie 21.
102Zadanie 22.
102Zadanie 26.
102Zadanie 27.
102Zadanie 28.
103Zadanie 29.
103Zadanie 32.
103Zadanie 33.
103Zadanie 34.
103Zadanie 36.
103
