W zadaniu musisz narysować wykres funkcji
![]() .
.
Dziedzina:
![]()
Rozwiązanie pierwszej nierówności:
![]()
![]()
![]()
Zatem
![]()
Z drugiego równania:
![]()
Dziedziną funkcji jest zatem:
![]()
![]()
Wykres funkcji logarytmicznej
![]() :
:
| x |
| 0 | 2 | 4 |
| y | 1 | 1 | -1 | -2 |
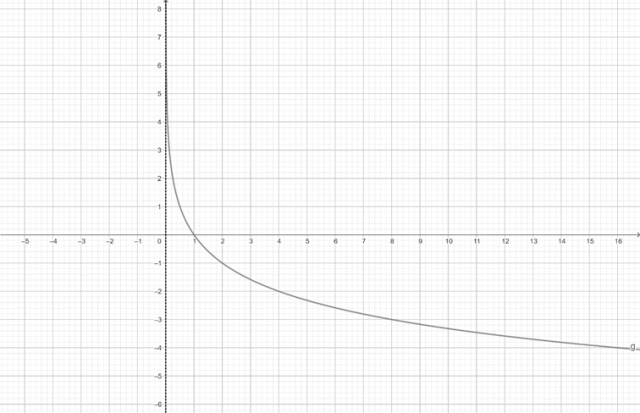
Wykres funkcji
![]() :
:
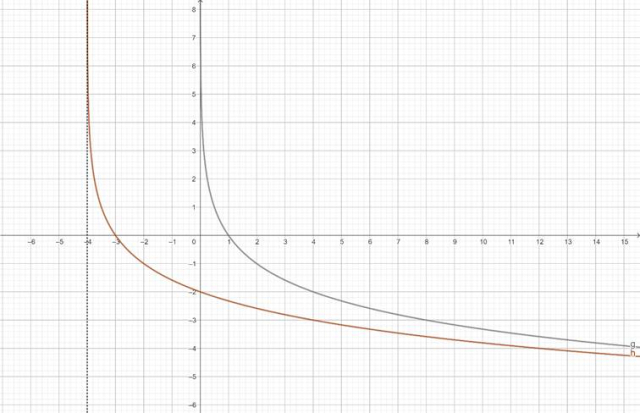
Wykres funkcji
![]() :
:
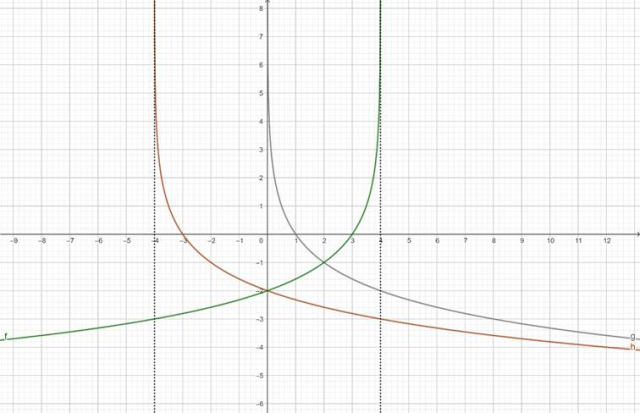
Wykres funkcji f:
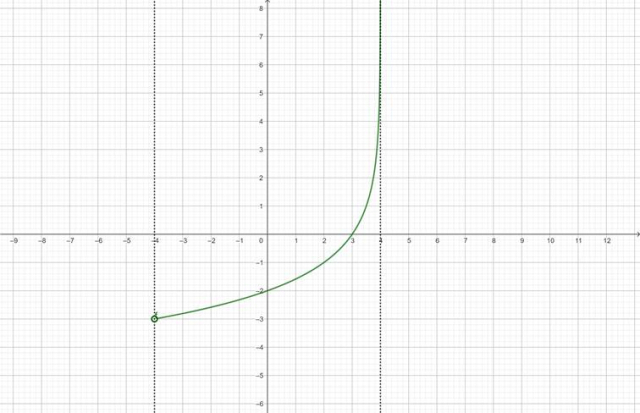

Wyznacz dziedzinę funkcji f:
![]()
Rozwiąż pierwszą nierówność:
![]()
![]()
![]()
Zatem
![]()
Z drugiego równania otrzymujesz, że:
![]()
Dziedziną funkcji jest zatem:
![]()
Sprowadź wzór funkcji f do jak najprostszej postaci. W tym celu skorzystaj z własności działań na logarytmach, a także wzoru skróconego mnożenia na różnicę kwadratów:
![]()
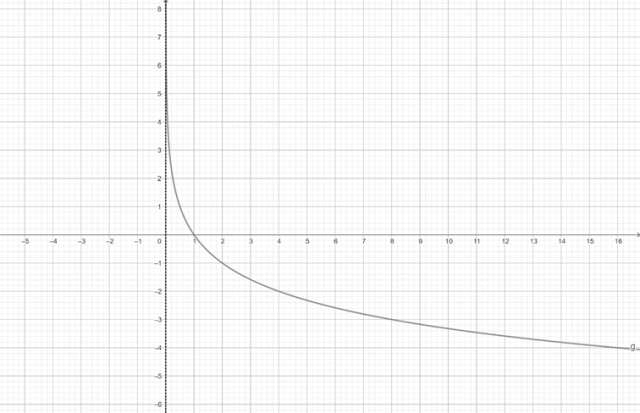
Aby narysować wykres funkcji f, zacznij od narysowania wykresu funkcji logarytmicznej
![]() poprzez znalezienie kilku charakterystycznych dla jej wykresu punktów:
poprzez znalezienie kilku charakterystycznych dla jej wykresu punktów:
| x |
| 0 | 2 | 4 |
| y | 1 | 1 | -1 | -2 |
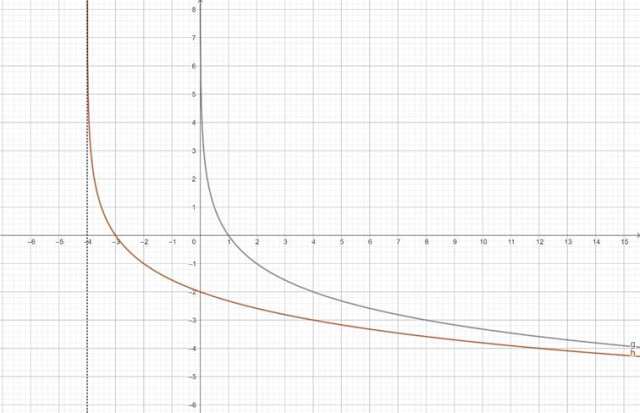
Następnie przesuń otrzymany wykres o 4 jednostki w lewo równolegle wzdłuż osi OX, aby otrzymać wykres funkcji:
![]()
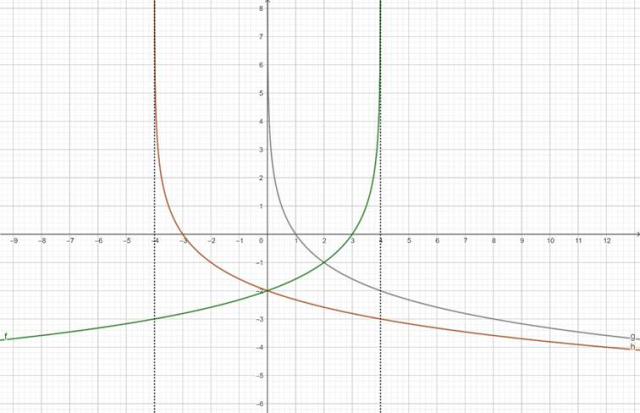
Odbij otrzymany wykres symetrycznie względem osi OY, aby otrzymać wykres funkcji f:
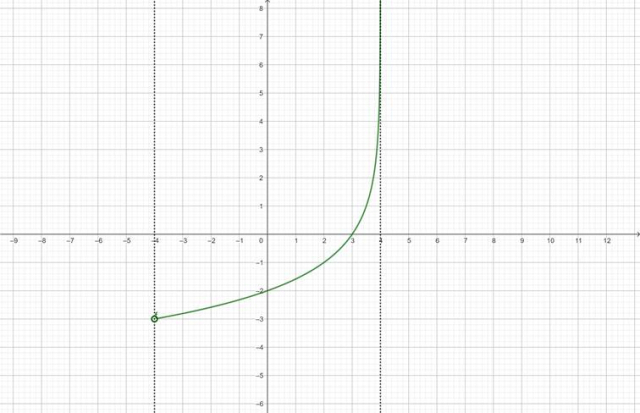
W ostatnim kroku zaznacz fragment wykresu, dla którego:
![]()

Ćwiczenie 1.
57Zadanie 1.
61Zadanie 2.
61Zadanie 3.
61Zadanie 4.
61Zadanie 5.
61Zadanie 6.
61Zadanie 7.
62Zadanie 9.
62Zadanie 16.
62Ćwiczenie 1.
64Zadanie 1.
68Zadanie 2.
68Zadanie 5.
69Zadanie 6.
69Zadanie 7.
69Zadanie 8.
69Zadanie 9.
69Zadanie 11.
69Zadanie 12.
69Zadanie 13.
70Zadanie 24.
70Zadanie 1.
77Zadanie 2.
77Zadanie 3.
77Zadanie 4.
77Zadanie 5.
77Zadanie 6.
77Zadanie 7.
77Zadanie 9.
78Zadanie 10.
78Zadanie 11.
78Zadanie 12.
78Zadanie 13.
78Zadanie 14.
78Zadanie 15.
78Zadanie 16.
78Zadanie 1.
83Zadanie 2.
84Zadanie 3.
84Zadanie 4.
84Zadanie 5.
84Zadanie 6.
84Zadanie 7.
84Zadanie 8.
85Zadanie 9.
85Zadanie 12.
85Zadanie 13.
85Zadanie 1.
91Zadanie 2.
92Zadanie 3.
92Zadanie 4.
92Zadanie 5.
92Zadanie 6.
92Zadanie 10.
92Zadanie 1.
98Zadanie 2.
99Zadanie 5.
99Zadanie 6.
99Zadanie 8.
99Zadanie 11.
101Zadanie 18.
101Zadanie 19.
101Zadanie 20.
102Zadanie 21.
102Zadanie 22.
102Zadanie 26.
102Zadanie 27.
102Zadanie 28.
103Zadanie 29.
103Zadanie 32.
103Zadanie 33.
103Zadanie 34.
103Zadanie 36.
103
