W zadaniu musisz rozwiązać nierówność
![]() .
.
![]() - sumaszeregu geometrycznego zbieżnego, gdzie
- sumaszeregu geometrycznego zbieżnego, gdzie
![]() oraz
oraz
![]() .
.
![]() , zatem:
, zatem:
![]()
![]()
![]()
Ponadto:
![]()
Zatem:
![]()
![]()
Czyli:
![]()
Wprowadź zmienną pomocniczą:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Zatem:
![]()
![]()
![]()
Czyli
![]()
![]() , zatem
, zatem
![]()

Zauważ, że po lewej stronie równania możesz skorzystać ze wzoru na sumę szeregu geometrycznego zbieżnego:
![]()
gdzie pierwszy wyraz szeregu
![]() oraz iloraz
oraz iloraz
![]() .
.
Dla szeregu zbieżnego
![]() , zatem:
, zatem:
![]()
![]()
Podstawa logarytmu jest większa od 1, a więc porównaj liczby logarytmowane, pozostawiając znak nierówności bez zmian:
![]()
Ponadto z własności logarytmu:
![]()
Zatem dziedziną nierówności jest:
![]()
Otrzymujesz zatem:
![]()
Nierówność możesz zapisać więc następująco:
![]()
Wprowadź zmienną pomocniczą:
![]()
Zapisz nierówność ze zmienną pomocniczą:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Rozwiąż nierówność kwadratową ze zmienną pomocniczą. Zacznij od wyznaczenia miejsc zerowych:
![]()
![]()
![]()
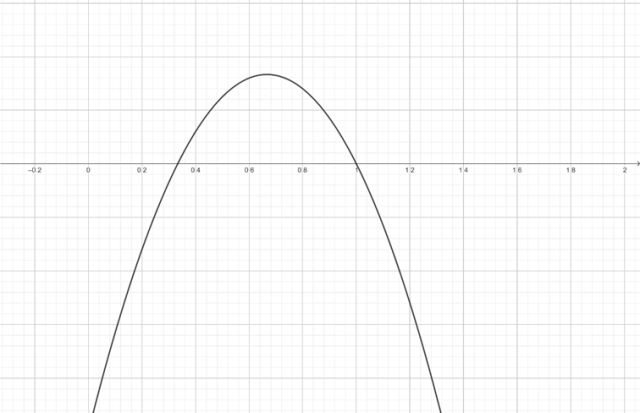
Narysuj wykres funkcji:
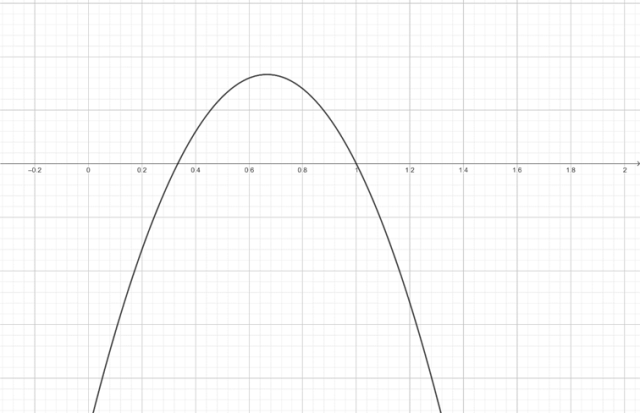
Z wykresu odczytaj, dla jakich argumentów funkcja przyjmuje wartości mniejsze od 0:
![]()
Zatem:
![]()
Zauważ, że:
![]()
Czyli:
![]()
Podstawa logarytmu jest większa od 1, a więc porównaj liczby logarytmowane, pozostawiając znak nierówności bez zmian:
![]()
Czyli
![]()
![]() , zatem
, zatem
![]()

Ćwiczenie 1.
57Zadanie 1.
61Zadanie 2.
61Zadanie 3.
61Zadanie 4.
61Zadanie 5.
61Zadanie 6.
61Zadanie 7.
62Zadanie 9.
62Zadanie 16.
62Ćwiczenie 1.
64Zadanie 1.
68Zadanie 2.
68Zadanie 5.
69Zadanie 6.
69Zadanie 7.
69Zadanie 8.
69Zadanie 9.
69Zadanie 11.
69Zadanie 12.
69Zadanie 13.
70Zadanie 24.
70Zadanie 1.
77Zadanie 2.
77Zadanie 3.
77Zadanie 4.
77Zadanie 5.
77Zadanie 6.
77Zadanie 7.
77Zadanie 9.
78Zadanie 10.
78Zadanie 11.
78Zadanie 12.
78Zadanie 13.
78Zadanie 14.
78Zadanie 15.
78Zadanie 16.
78Zadanie 1.
83Zadanie 2.
84Zadanie 3.
84Zadanie 4.
84Zadanie 5.
84Zadanie 6.
84Zadanie 7.
84Zadanie 8.
85Zadanie 9.
85Zadanie 12.
85Zadanie 13.
85Zadanie 1.
91Zadanie 2.
92Zadanie 3.
92Zadanie 4.
92Zadanie 5.
92Zadanie 6.
92Zadanie 10.
92Zadanie 1.
98Zadanie 2.
99Zadanie 5.
99Zadanie 6.
99Zadanie 8.
99Zadanie 11.
101Zadanie 18.
101Zadanie 19.
101Zadanie 20.
102Zadanie 21.
102Zadanie 22.
102Zadanie 26.
102Zadanie 27.
102Zadanie 28.
103Zadanie 29.
103Zadanie 32.
103Zadanie 33.
103Zadanie 34.
103Zadanie 36.
103
