W zadaniu musisz znaleźć wartości parametru m,
![]() , dla których dziedziną funkcji
, dla których dziedziną funkcji
![]() jest zbiór R.
jest zbiór R.
![]()
W zadaniu muszą zostać rozpatrzone dwa przypadki – dla
![]() oraz
oraz
![]()
Jeżeli
![]() , to:
, to:
![]()
Dla
![]() :
:
![]()
![]()
![]()
Zbiorem rozwiązań nie jest zbiór liczb rzeczywistych, zatem
![]() nie spełnia warunków zadania.
nie spełnia warunków zadania.
Dla
![]()
![]()
![]()
![]() spełnia zatem warunki zadania, czyli:
spełnia zatem warunki zadania, czyli:
![]()
Dla
![]() :
:
![]()
![]() – warunki
– warunki
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Poza tym:
![]()
Rozwiązanie pierwszej nierówności:
![]()
Rozwiązanie drugiej nierówności:
![]()
![]()
Czyli
![]()
Część wspólna przedziałów z drugiego przypadku:
![]()
Czyli
![]()
Suma przedziałów z obu rozpatrywanych przypadków:
![]()
Zatem dla
![]() dziedziną funkcji f jest zbiór liczb rzeczywistych.
dziedziną funkcji f jest zbiór liczb rzeczywistych.

Funkcja f jest funkcją logarytmiczną, czyli ma postać:
![]() gdzie
gdzie
![]()
W zadaniu:
![]()
Musisz zatem obliczyć wartości parametru m, dla których nierówność:
![]()
będzie spełniona przez wszystkie liczby rzeczywiste x. Rozpatrz dwa przypadki – dla
![]() oraz
oraz
![]()
Jeżeli
![]() , to:
, to:
![]() , czyli otrzymujesz dwie nierówności:
, czyli otrzymujesz dwie nierówności:
Dla
![]() :
:
![]()
![]()
![]()
Zbiorem rozwiązań nie jest zbiór liczb rzeczywistych, zatem
![]() nie spełnia warunków zadania.
nie spełnia warunków zadania.
Dla
![]()
![]()
![]()
Nierówność jest prawdziwa, czyli zbiorem rozwiązań nierówności jest zbiór liczb rzeczywistych. Oznacza to, że
![]() spełnia warunki zadania, czyli:
spełnia warunki zadania, czyli:
![]()
Rozważ drugi przypadek dla
![]() . Wtedy nierówność kwadratowa:
. Wtedy nierówność kwadratowa:
![]()
będzie spełniona przez wszystkie liczby rzeczywiste, jeśli parabola będzie miała ramiona skierowane w górę oraz funkcja nie będzie mieć miejsc zerowych, czyli:
![]()
Oblicz, dla jakich argumentów funkcja nie posiada miejsc zerowych:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
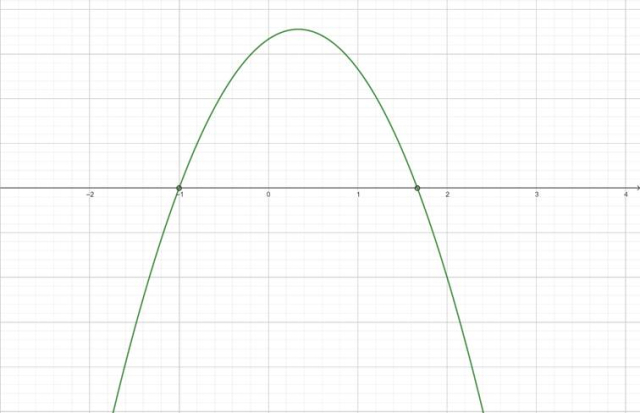
Narysuj wykres funkcji:
Z wykresu odczytaj, dla jakich m funkcja przyjmuje wartości mniejsze od 0:
![]()
Z pozostałych dwóch warunków tego przypadku wynika, że
![]() , zatem z pierwszej nierówności:
, zatem z pierwszej nierówności:
![]()
I z drugiej:
![]()
![]()
Czyli
![]()
Z drugiego przypadku otrzymujesz zatem, że:
![]()
Czyli
![]()
Znajdź sumę znalezionych przedziałów z dwóch rozpatrywanych przypadków:
![]()
Zatem dla
![]() dziedziną funkcji f jest zbiór liczb rzeczywistych.
dziedziną funkcji f jest zbiór liczb rzeczywistych.

Ćwiczenie 1.
57Zadanie 1.
61Zadanie 2.
61Zadanie 3.
61Zadanie 4.
61Zadanie 5.
61Zadanie 6.
61Zadanie 7.
62Zadanie 9.
62Zadanie 16.
62Ćwiczenie 1.
64Zadanie 1.
68Zadanie 2.
68Zadanie 5.
69Zadanie 6.
69Zadanie 7.
69Zadanie 8.
69Zadanie 9.
69Zadanie 11.
69Zadanie 12.
69Zadanie 13.
70Zadanie 24.
70Zadanie 1.
77Zadanie 2.
77Zadanie 3.
77Zadanie 4.
77Zadanie 5.
77Zadanie 6.
77Zadanie 7.
77Zadanie 9.
78Zadanie 10.
78Zadanie 11.
78Zadanie 12.
78Zadanie 13.
78Zadanie 14.
78Zadanie 15.
78Zadanie 16.
78Zadanie 1.
83Zadanie 2.
84Zadanie 3.
84Zadanie 4.
84Zadanie 5.
84Zadanie 6.
84Zadanie 7.
84Zadanie 8.
85Zadanie 9.
85Zadanie 12.
85Zadanie 13.
85Zadanie 1.
91Zadanie 2.
92Zadanie 3.
92Zadanie 4.
92Zadanie 5.
92Zadanie 6.
92Zadanie 10.
92Zadanie 1.
98Zadanie 2.
99Zadanie 5.
99Zadanie 6.
99Zadanie 8.
99Zadanie 11.
101Zadanie 18.
101Zadanie 19.
101Zadanie 20.
102Zadanie 21.
102Zadanie 22.
102Zadanie 26.
102Zadanie 27.
102Zadanie 28.
103Zadanie 29.
103Zadanie 32.
103Zadanie 33.
103Zadanie 34.
103Zadanie 36.
103
