W zadaniu musisz obliczyć wartość a występującą we wzorze funkcji logarytmicznej
, gdzie
oraz
, wiedząc, że do wykresu funkcji należy punkt
, a następnie narysować wykres funkcji f i na jego podstawie podać zbiór wartości x, dla których funkcja przyjmuje wartości mniejsze od 3.
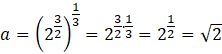
Zatem:
Wykres funkcji f:
| x |
|
| 1 | 2 |
|
| y | -4 | -2 | 0 | 2 | 3 |
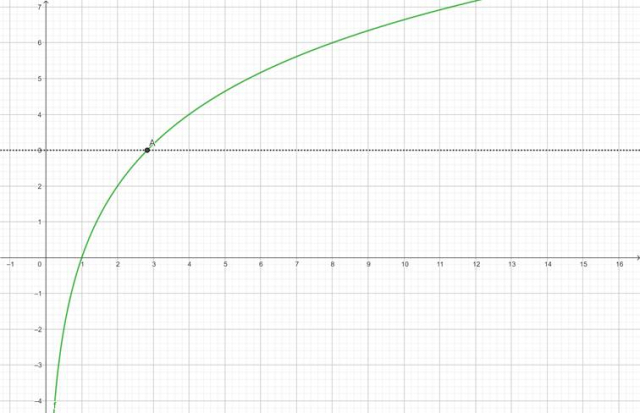
Szukana funkcja jest funkcją logarytmiczną, czyli ma postać:
, gdzie
oraz
Do wykresu funkcji należy punkt
, czyli:
Musisz zatem rozwiązać równanie:
Skorzystaj z definicji logarytmu:
Podnieś obie strony równania do potęgi:
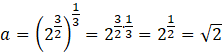
Aby otrzymać wzór funkcji, wstaw znalezione a pod wzór
:
Narysuj wykres funkcji logarytmicznej f poprzez znalezienie kilku charakterystycznych dla niej punktów. Pamiętaj, że
.
| x |
|
| 1 | 2 |
|
| y | -4 | -2 | 0 | 2 | 3 |
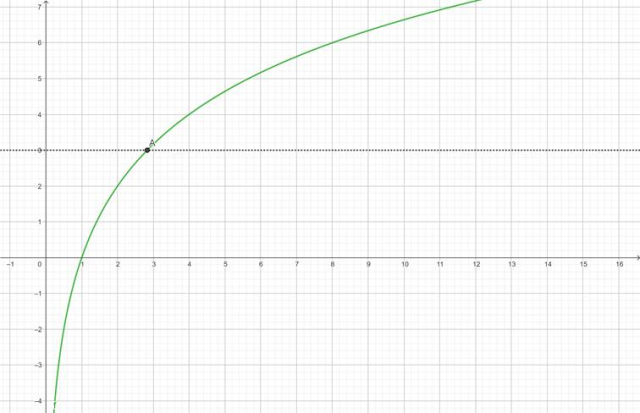
Z wykresu odczytaj, dla jakich x funkcja przyjmuje wartości mniejsze od 3:
Ćwiczenie 1.
57Zadanie 1.
61Zadanie 2.
61Zadanie 3.
61Zadanie 4.
61Zadanie 5.
61Zadanie 6.
61Zadanie 7.
62Zadanie 9.
62Zadanie 16.
62Ćwiczenie 1.
64Zadanie 1.
68Zadanie 2.
68Zadanie 5.
69Zadanie 6.
69Zadanie 7.
69Zadanie 8.
69Zadanie 9.
69Zadanie 11.
69Zadanie 12.
69Zadanie 13.
70Zadanie 24.
70Zadanie 1.
77Zadanie 2.
77Zadanie 3.
77Zadanie 4.
77Zadanie 5.
77Zadanie 6.
77Zadanie 7.
77Zadanie 9.
78Zadanie 10.
78Zadanie 11.
78Zadanie 12.
78Zadanie 13.
78Zadanie 14.
78Zadanie 15.
78Zadanie 16.
78Zadanie 1.
83Zadanie 2.
84Zadanie 3.
84Zadanie 4.
84Zadanie 5.
84Zadanie 6.
84Zadanie 7.
84Zadanie 8.
85Zadanie 9.
85Zadanie 12.
85Zadanie 13.
85Zadanie 1.
91Zadanie 2.
92Zadanie 3.
92Zadanie 4.
92Zadanie 5.
92Zadanie 6.
92Zadanie 10.
92Zadanie 1.
98Zadanie 2.
99Zadanie 5.
99Zadanie 6.
99Zadanie 8.
99Zadanie 11.
101Zadanie 18.
101Zadanie 19.
101Zadanie 20.
102Zadanie 21.
102Zadanie 22.
102Zadanie 26.
102Zadanie 27.
102Zadanie 28.
103Zadanie 29.
103Zadanie 32.
103Zadanie 33.
103Zadanie 34.
103Zadanie 36.
103