W zadaniu musisz znaleźć dziedzinę funkcji f określonej wzorem
![]() , a następnie znaleźć argumenty, dla których funkcja f przyjmuje wartości nie większe niż jeden.
, a następnie znaleźć argumenty, dla których funkcja f przyjmuje wartości nie większe niż jeden.
Dziedzina:
![]()
![]()
Pierwsza nierówność:
![]()
![]()
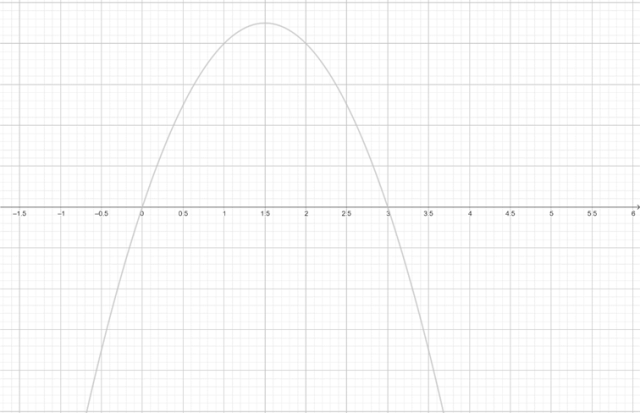
![]()
Zatem:
![]()
![]()
![]()
Wykres funkcji
![]() narysowany na podstawie funkcji logarytmicznej
narysowany na podstawie funkcji logarytmicznej
![]() :
:
| x |
| 1 | 2 | 4 |
| Y | -1 | 0 | 1 | 2 |
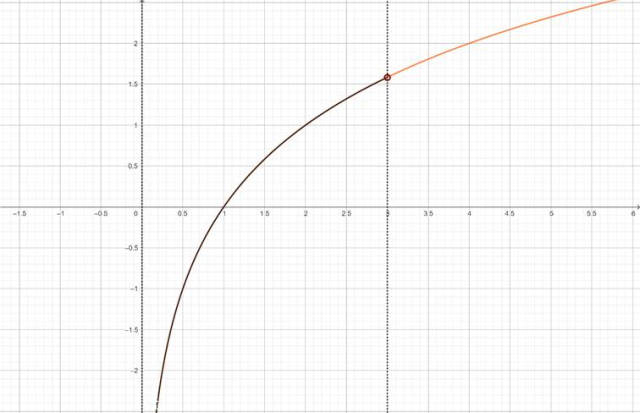
![]()

Wyznacz dziedzinę funkcji:
![]()
![]()
Rozwiąż pierwszą nierówność. W tym celu znajdź miejsca zerowe funkcji kwadratowej i narysuj jej wykres:
![]()
![]()
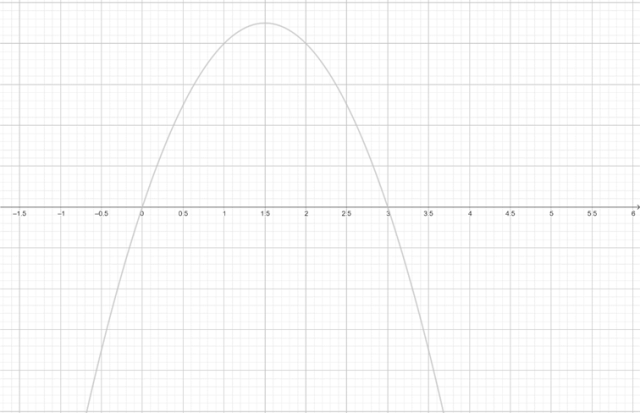
Z wykresu odczytaj, dla jakich argumentów funkcja przyjmuje wartości większe od 0:
![]()
Czyli otrzymujesz:
![]()
Zatem:
![]()
Korzystając z własności działań na logarytmach, przekształć wzór funkcji f:
![]()
Narysuj wykres funkcji
![]() . W tym celu narysuj wykres funkcji logarytmicznej
. W tym celu narysuj wykres funkcji logarytmicznej
![]() poprzez znalezienie kilku charakterystycznych dla niej punktów, a następnie zaznacz fragment wykresu dla
poprzez znalezienie kilku charakterystycznych dla niej punktów, a następnie zaznacz fragment wykresu dla
![]() .
.
| X |
| 1 | 2 | 4 |
| Y | -1 | 0 | 1 | 2 |
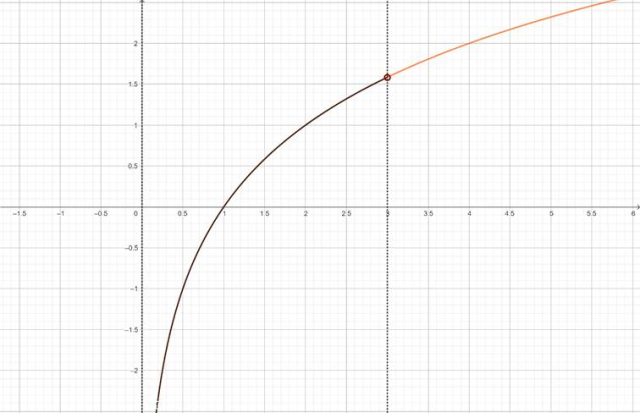
Z wykresu odczytaj, dla jakich argumentów funkcja f przyjmuje wartości nie większe niż 1:
![]()

Ćwiczenie 1.
57Zadanie 1.
61Zadanie 2.
61Zadanie 3.
61Zadanie 4.
61Zadanie 5.
61Zadanie 6.
61Zadanie 7.
62Zadanie 9.
62Zadanie 16.
62Ćwiczenie 1.
64Zadanie 1.
68Zadanie 2.
68Zadanie 5.
69Zadanie 6.
69Zadanie 7.
69Zadanie 8.
69Zadanie 9.
69Zadanie 11.
69Zadanie 12.
69Zadanie 13.
70Zadanie 24.
70Zadanie 1.
77Zadanie 2.
77Zadanie 3.
77Zadanie 4.
77Zadanie 5.
77Zadanie 6.
77Zadanie 7.
77Zadanie 9.
78Zadanie 10.
78Zadanie 11.
78Zadanie 12.
78Zadanie 13.
78Zadanie 14.
78Zadanie 15.
78Zadanie 16.
78Zadanie 1.
83Zadanie 2.
84Zadanie 3.
84Zadanie 4.
84Zadanie 5.
84Zadanie 6.
84Zadanie 7.
84Zadanie 8.
85Zadanie 9.
85Zadanie 12.
85Zadanie 13.
85Zadanie 1.
91Zadanie 2.
92Zadanie 3.
92Zadanie 4.
92Zadanie 5.
92Zadanie 6.
92Zadanie 10.
92Zadanie 1.
98Zadanie 2.
99Zadanie 5.
99Zadanie 6.
99Zadanie 8.
99Zadanie 11.
101Zadanie 18.
101Zadanie 19.
101Zadanie 20.
102Zadanie 21.
102Zadanie 22.
102Zadanie 26.
102Zadanie 27.
102Zadanie 28.
103Zadanie 29.
103Zadanie 32.
103Zadanie 33.
103Zadanie 34.
103Zadanie 36.
103
