W tym zadaniu należy narysować zbiór rozwiązań dla równania:
. Zbiór przedstaw na układzie współrzędnych.
Obie strony należy podnieść do kwadratu ze względu na to, że są nieujemne.
Rozpatrujemy 4 przypadki:
1:
Cała I ćwiartka spełnia układ.
2:
Cała II ćwiartka nie spełnia układu.
3:
Cała III ćwiartka spełnia układ.
4:
Cała IV ćwiartka spełnia układu.
Dodatkowo punkt (0,0) spełnia warunek układu.
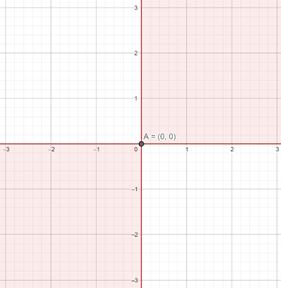
W tym zadaniu należy graficznie rozwiązać równanie, więc zaczniemy od zredukowania ilości wartości bezwzględnej. Podnieśmy obie strony do kwadratu. Skorzystamy z zależności
i wzoru skróconego mnożenia
. Teraz Musisz rozpatrzeć równanie na 4 sposoby. W każdym przypadku rysujemy wykres
– pamiętaj, aby rysować go tylko w danym przedziale np. x > 0 i y > 0. Po rozpatrzeniu 4 możliwości tworzymy część wspólną, która jest rozwiązaniem naszego równania. Zwróć uwagę, że punkt (0,0) spełnia równanie, więc uwzględniamy go na wykresie.