W tym zadaniu wykaż, że
jest prawdziwe dla każdych a i b dodatnich.
Z:
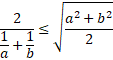
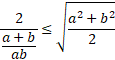
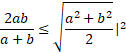
Wniosek: skoro z założenia:
, to
i
, ponieważ kwadrat dowolnej liczby jest większy lub równy zero – co za tym idzie, ich suma jest również większa lub równa 0.
Zamień ułamek po lewej stronie na dwupiętrowy, a następnie podnieś obie strony do kwadratu. Sprowadź ułamki do wspólnego mianownika i pomnóż obustronnie przez mianownik, który jest większy od zera, ponieważ z założenia
. Rozłóż niektóre wyrażenia na czynniki i zrób 2 wzory skróconego mnożenia. Zauważ, że
jest większe lub równe zero, ponieważ jest to wyrażenie podniesione do 2 potęgi. Wyrażenie
to iloczyn dodatnich liczb, a więc jest on nieujemny. Suma 2 większych lub równych zeru liczb jest większa lub równa zero, co kończy dowód.