W tym zadaniu oblicz czas, po jakim czasie ciśnienie w pojemniku o objętości V = 200 cm3 zmaleje o q = 1%, jeśli panują w nim warunki normalne (T0 = 273 K, p0 = 1013 hPa), a powietrze wydostaje się na zewnątrz w ilości ![]()
Z równania Clapeyrona liczba cząstek, która wydostanie się z pojemnika:
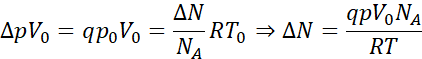
Więc wydostaną się one z pojemnika w czasie:
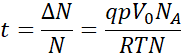
Podstawiając wartości liczbowe:
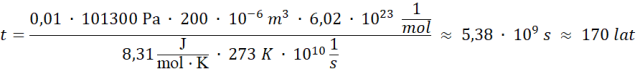
Odpowiedź: Ciśnienie w pojemniku zmniejszy się o 1% po około 170 latach.

Korzystamy z równania Clapeyrona dla różnicy ciśnienia, gdzie zmianę liczby moli zapisujemy jako iloraz zmiany liczby cząsteczek i liczby Avogadra. Czas, po jakim zmniejszy się ciśnienie, jest równe ilorazowi wyznaczonej zmiany liczby cząsteczek i tempa ucieczki cząsteczek.

Przykład Przykład 1.
75Przykład Przykład 2.
76Przykład Przykład 3.
79Przykład Przykład 4.
81Przykład Przykład 5.
83Przykład Przykład 6.
84Zadanie 8.1.3.
86Zadanie 8.1.4.
87Zadanie 8.1.5.
87Zadanie 8.1.6.
87Zadanie 8.1.8.
88Zadanie 8.1.9.
89Zadanie 8.1.10.
89Zadanie 8.1.15.
90Zadanie 8.1.21.
91Zadanie 8.1.24.
91Zadanie 8.1.25.
92Zadanie 8.1.28.
92Zadanie 8.1.30.
93Zadanie 8.1.33.
93Przykład Przykład 1.
94Przykład Przykład 2.
95Przykład Przykład 3.
97Zadanie 8.2.5.
99Zadanie 8.2.8.
100Zadanie 8.2.11.
100Zadanie 8.2.13.
100Zadanie 8.2.14.
101Zadanie 8.2.15.
101Przykład Przykład 3.
103Przykład Przykład 4.
106Zadanie 8.3.7.
108Zadanie 8.3.9.
109Zadanie 8.3.10.
109Zadanie 8.3.11.
109Przykład Przykład
110Zadanie 8.4.2.
112Przykład Przykład. Balon
116Zadanie Zadanie 1. Cykl przemian
118Zadanie Zadanie 2. Silnik spalinowy
118Zadanie Zadanie 3. Cząsteczki gazu
119
