W tym zadaniu oblicz położenie ruchomego tłoka, oddzielającego o masie molowej ![]()
![]()
Zapisujemy równanie Clapeyrona dla obu części naczynia dla tłoka w położeniu x, liczbę moli gazu przedstawiamy jako iloraz masy i masy molowej gazu:
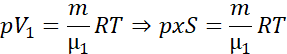
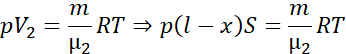
Dzielimy równania stronami:
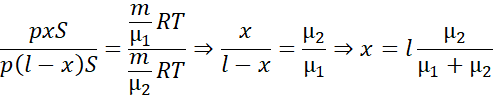
Podstawiając wartości liczbowe:
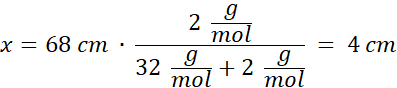
Odpowiedź: Tłok powinien znajdować się w takim położeniu, że część naczynia, w której znajduje się tlen, ma 4 cm długości.

Zapisujemy liczbę moli jako iloraz masy gazu i masy molowej, a objętość jako iloczyn powierzchni przekroju i długości części naczynia. Jeśli jedna część naczynia ma długość x, to druga musi mieć długość l – x. Zapisujemy równanie Clapeyrona dla obu części naczynia i dzielimy równania stronami.

Przykład Przykład 1.
75Przykład Przykład 2.
76Przykład Przykład 3.
79Przykład Przykład 4.
81Przykład Przykład 5.
83Przykład Przykład 6.
84Zadanie 8.1.3.
86Zadanie 8.1.4.
87Zadanie 8.1.5.
87Zadanie 8.1.6.
87Zadanie 8.1.8.
88Zadanie 8.1.9.
89Zadanie 8.1.10.
89Zadanie 8.1.15.
90Zadanie 8.1.21.
91Zadanie 8.1.24.
91Zadanie 8.1.25.
92Zadanie 8.1.28.
92Zadanie 8.1.30.
93Zadanie 8.1.33.
93Przykład Przykład 1.
94Przykład Przykład 2.
95Przykład Przykład 3.
97Zadanie 8.2.5.
99Zadanie 8.2.8.
100Zadanie 8.2.11.
100Zadanie 8.2.13.
100Zadanie 8.2.14.
101Zadanie 8.2.15.
101Przykład Przykład 3.
103Przykład Przykład 4.
106Zadanie 8.3.7.
108Zadanie 8.3.9.
109Zadanie 8.3.10.
109Zadanie 8.3.11.
109Przykład Przykład
110Zadanie 8.4.2.
112Przykład Przykład. Balon
116Zadanie Zadanie 1. Cykl przemian
118Zadanie Zadanie 2. Silnik spalinowy
118Zadanie Zadanie 3. Cząsteczki gazu
119
