Udowodnij, że wielomian 4x4 + 8x3–5x2–2x + 1 posiada dwa pierwiastki wymierne i dwa pierwiastki niewymierne i wyznacz je.
W(x) = 4x4 + 8x3–5x2–2x + 1,
st W(x) = 4
W(x)–wszystkie współczynniki całkowite
p = 1
q = 4
Liczba p–całkowity dzielnik liczby 1 tylko, jeśli p ∊ {–1, 1}
Liczba q–całkowity dzielnik liczby 4, tylko dla q ∊ {–4,–2,–1, 1, 2, 4}
Wielomian W(x) ma pierwiastki wymierne, które należą do zbioru:
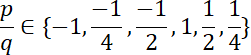
![]()
![]()
![]()
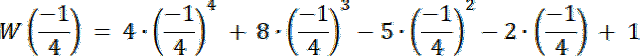
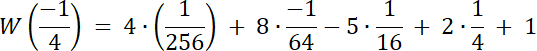
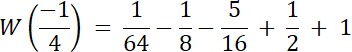
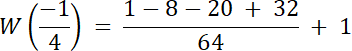
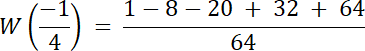
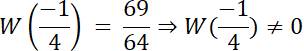
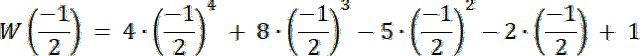
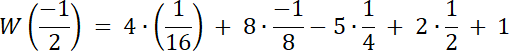
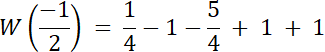
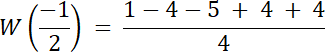
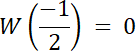
![]()
![]()
![]()
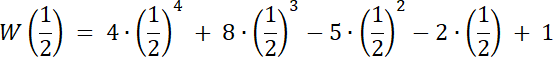
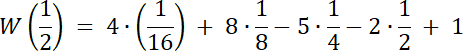
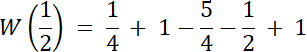
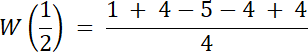
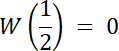
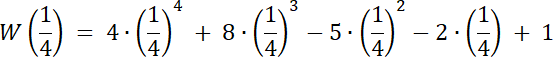
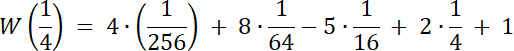
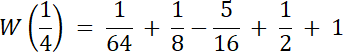
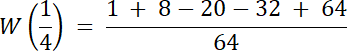
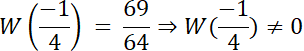
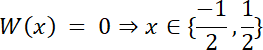
Skoro st. W(x) = 4, a wiemy, że W(x) dla dwóch liczb wymiernych, to 2 pierwiastki tego równania to liczby niewymierne.
W(x) = a4x4 + a3x3 + a2x2 + a1x + a0
a4 = 4, a3 = 8, a2 = –5, a1 = –2, a0 = 1
dla c = 0,5
| W(x) | a4 | a3 | a2 | a1 | ao |
| 0,5 | 4 | 8 | –5 | –2 | 1 |
| 4 | 10 | 0 | –2 | 0 | |
| Q(x) | b3 | b2 | b1 | b0 | r |
b3 = a4
b2 = a3 + c∙b3
b1 = a2 + c∙b2
bo = a1 + c∙b1
r = ao + c∙b0
W(x) = (x–0,5)(4x3 + 10x2–2)
W1(x) = (4x3 + 10x2–2)
W1(x) = a3x3 + a2x2 + a1x + a0
a3 = 4, a2 = 10, a1 = 0, a0 = –2
dla c = –0,5
| W(x) | a3 | a2 | a1 | ao |
| –0,5 | 4 | 10 | 0 | –2 |
| 4 | 8 | –4 | 0 | |
| Q(x) | b2 | b1 | b0 | r |
b2 = a3
b1 = a2 + c∙b2
bo = a1 + c∙b1
r = ao + c∙b0
W1(x) = 4x2–6x–10
W1(x) = (x + 0,5)(4x2 + 8x–4)
W1(x) = 0⇒ 4x2 + 8x–4 = 0
4x2 + 8x–4 = 0 /4
x2 + 2x–1 = 0
∆ = (2)2–4∙1∙(–1)
∆ = 4 + 4
∆ = 8
√∆ = 2√2
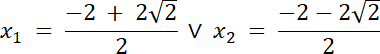
![]()

W tym zadaniu na początek skorzystaj z twierdzenia o pierwiastkach wymiernych wielomianu, następnie je wyznacz. W kolejnym kroku ze schematu Hornera wyznacz wyrażenie kwadratowe tego równania, a na koniec wyznacz pierwiastki równania kwadratowego.

Zadanie 1.
264Zadanie 2.
264Zadanie 3.
265Zadanie 4.
265Zadanie 5.
265Zadanie 7.
265Zadanie 10.
265Ćwiczenie 1.
266Ćwiczenie 2.
267Zadanie 1.
269Zadanie 2.
269Zadanie 3.
269Zadanie 4.
269Zadanie 5.
269Zadanie 6.
269Zadanie 7.
269Zadanie 8.
269Zadanie 9.
269Zadanie 1.
272Zadanie 2.
272Zadanie 3.
272Zadanie 4.
272Zadanie 5.
272Zadanie 6.
272Zadanie 7.
272Ćwiczenie 3.
274Ćwiczenie 4.
274Ćwiczenie 6.
276Ćwiczenie 7.
277Zadanie 1.
277Zadanie 2.
278Zadanie 3.
278Zadanie 4.
278Zadanie 5.
278Zadanie 6.
278Zadanie 7.
278Zadanie 8.
278Zadanie 9.
278Zadanie 1.
283Zadanie 3.
283Zadanie 4.
284Zadanie 5.
284Zadanie 13.
284Ćwiczenie 4.
286Zadanie 1.
290Zadanie 2.
290Zadanie 3.
290Zadanie 4.
290Zadanie 5.
290Zadanie 6.
290Ćwiczenie 4.
294Zadanie 1.
295Zadanie 2.
296Zadanie 3.
296Zadanie 4.
296Zadanie 5.
296Zadanie 6.
296Zadanie 7.
296Zadanie 8.
296Zadanie 9.
296Zadanie 10.
296Zadanie 1.
301Zadanie 2.
301Zadanie 3.
301Zadanie 6.
302Zadanie 7.
302Zadanie 9.
302Zadanie 11.
302Zadanie 12.
302Zadanie 13.
302Ćwiczenie 2.
304Ćwiczenie 3.
305Zadanie 1.
306Zadanie 2.
306Zadanie 3.
307Zadanie 4.
307Zadanie 5.
307Zadanie 6.
307Zadanie 7.
307Zadanie 8.
307Zadanie 9.
307Zadanie 10.
307Ćwiczenie 1.
308Zadanie 1.
310Zadanie 2.
310Zadanie 3.
311Zadanie 4.
311Zadanie 5.
311Zadanie 6.
311Zadanie 7.
311Zadanie 8.
311Zadanie 9.
311Zadanie 10.
311Zadanie 17.
315Zadanie 18.
315Zadanie 24.
315Zadanie 26.
315Zadanie 28.
315
