W tym zadaniu wyznacz wszystkie wymierne pierwiastki wielomianu W(x).
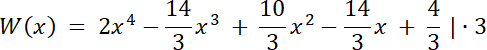
![]()
![]()
Sprawdź, czy wielomian nie ma przypadkiem pierwiastka całkowitego
a0 = 2
Dzielniki wyrazu wolnego: {–2,–1, 1, 2}
![]()
W(2) = 2(3∙(2)4–7∙(2)3 + 5∙(2)2–7∙(2) + 2)
W(2) = 2(3∙16–7∙8 + 5∙4–14 + 2)
W(2) = 2(48–56 + 20–14 + 2)
W(2) = 0
W(x) = a4x4 + a3x3 + a2x2 + a1x + a0
a4 = 3, a3 = –7, a2 = 5, a1 = –7, a0 = 2
dla c = 2
| W(x) | a4 | a3 | a2 | a1 | ao |
| 2 | 3 | –7 | 5 | –7 | 2 |
| 3 | –1 | 3 | –1 | 0 | |
| Q(x) | b3 | b2 | b1 | b0 | r |
b3 = a4
b2 = a3 + c∙b3
b1 = a2 + c∙b2
bo = a1 + c∙b1
r = ao + c∙b0
W(x) = (x–2)(3x3–x2 + 3x–1)
W(x) = (x–2)(3x(x2 + 1)–(x2 + 1))
W(x) = (x–2)(3x–1)(x2 + 1)
W(x) = 0
(x–2)(3x–1)(x2 + 1) = 0
x–2 = 0 v 3x–1 = 0 v x2 + 1 = 0
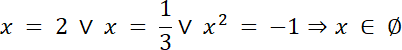
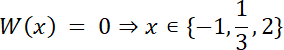

Na początku, wymnóż wielomian przez liczbę 3, by pozbyć się ułamków z mianownika, następnie skorzystaj z twierdzenia o pierwiastkach całkowitych wielomianu w(x) i sprawdź, czy wielomian ten, posiada taki pierwiastek. Skorzystaj ze schematu Hornera, aby wyznaczyć wyrażenie stopnia 3, które jest ilorazem wyrażeń W(x), (x–2)–twierdzenie Bezout, a następnie zauważ, że wyrażenie w wielomianie można pogrupować. Na koniec wyznacz z postaci iloczynowej wielomianu W(x) jego pierwiastki.

Zadanie 1.
264Zadanie 2.
264Zadanie 3.
265Zadanie 4.
265Zadanie 5.
265Zadanie 7.
265Zadanie 10.
265Ćwiczenie 1.
266Ćwiczenie 2.
267Zadanie 1.
269Zadanie 2.
269Zadanie 3.
269Zadanie 4.
269Zadanie 5.
269Zadanie 6.
269Zadanie 7.
269Zadanie 8.
269Zadanie 9.
269Zadanie 1.
272Zadanie 2.
272Zadanie 3.
272Zadanie 4.
272Zadanie 5.
272Zadanie 6.
272Zadanie 7.
272Ćwiczenie 3.
274Ćwiczenie 4.
274Ćwiczenie 6.
276Ćwiczenie 7.
277Zadanie 1.
277Zadanie 2.
278Zadanie 3.
278Zadanie 4.
278Zadanie 5.
278Zadanie 6.
278Zadanie 7.
278Zadanie 8.
278Zadanie 9.
278Zadanie 1.
283Zadanie 3.
283Zadanie 4.
284Zadanie 5.
284Zadanie 13.
284Ćwiczenie 4.
286Zadanie 1.
290Zadanie 2.
290Zadanie 3.
290Zadanie 4.
290Zadanie 5.
290Zadanie 6.
290Ćwiczenie 4.
294Zadanie 1.
295Zadanie 2.
296Zadanie 3.
296Zadanie 4.
296Zadanie 5.
296Zadanie 6.
296Zadanie 7.
296Zadanie 8.
296Zadanie 9.
296Zadanie 10.
296Zadanie 1.
301Zadanie 2.
301Zadanie 3.
301Zadanie 6.
302Zadanie 7.
302Zadanie 9.
302Zadanie 11.
302Zadanie 12.
302Zadanie 13.
302Ćwiczenie 2.
304Ćwiczenie 3.
305Zadanie 1.
306Zadanie 2.
306Zadanie 3.
307Zadanie 4.
307Zadanie 5.
307Zadanie 6.
307Zadanie 7.
307Zadanie 8.
307Zadanie 9.
307Zadanie 10.
307Ćwiczenie 1.
308Zadanie 1.
310Zadanie 2.
310Zadanie 3.
311Zadanie 4.
311Zadanie 5.
311Zadanie 6.
311Zadanie 7.
311Zadanie 8.
311Zadanie 9.
311Zadanie 10.
311Zadanie 17.
315Zadanie 18.
315Zadanie 24.
315Zadanie 26.
315Zadanie 28.
315
