W tym zadaniu musisz obliczyć pierwiastki całkowite wielomianu W(x).
W(x) = 6x4 + x3–16x2 + 11x–2
Wszystkie współczynniki wielomianu W(x) są liczbami całkowitymi, sprawdźmy, czy pierwiastek wielomianu W(x) nie jest może liczbą całkowitą
Sprawdźmy najpierw, czy pierwiastek W(x) nie jest liczbą całkowitą:
Dzielniki liczby 2:{–2,–1, 1, 2}
W(1) = 6∙14 + 13–16∙12 + 11∙1–2
W(1) = 6 + 1–16 + 11–2
W(1) = 0
W(x) = a4x4 + a3x3 + a2x2 + a1x + a0
a4 = 6, a3 = 1, a2 = –16, a1 = 11, a0 = –2
dla c = 1
| W(x) | a4 | a3 | a2 | a1 | ao |
| 1 | 6 | 1 | –16 | 11 | –2 |
| 6 | 7 | –9 | 2 | 0 | |
| Q(x) | b3 | b2 | b1 | b0 | r |
b3 = a4
b2 = a3 + c∙b3
b1 = a2 + c∙b2
bo = a1 + c∙b1
r = ao + c∙b0
W(x) = (x–1)(6x3 + 7x2–9x + 2)
W(x) = (x–1)∙W1(x)
W1(x) = (6x3 + 7x2–9x + 2)
Współczynniki wielomianu W1(x) również są liczbami całkowitymi, sprawdźmy, czy pierwiastkiem wielomianu W1(x) nie jest liczba całkowita
x = –2
W1(–2) = 6∙(–2)3 + 7∙(–2)2–9∙(–2) + 2
W1(–2) = 6∙(–8) + 7∙(4)–9∙(–2) + 2
W1(–2) = –48 + 28 + 18 + 2
W1(–2) = 0
W1(x) = a3x3 + a2x2 + a1x + a0
a3 = 6, a2 = 7, a1 = –9, a0 = 2
dla c = –2
| W(x) | a3 | a2 | a1 | a0 |
| –2 | 6 | 7 | –9 | 2 |
| 6 | –5 | –1 | 0 | |
| Q(x) | b2 | b1 | b0 | r |
b2 = a3
b1 = a2 + c∙b2
bo = a1 + c∙b1
r = ao + c∙b0
W2(x) = (x + 2)∙W1(x)
W2(x) = 6x2–5x + 1
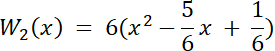
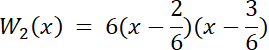
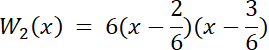
W(x) = (x + 2)(x–1)∙W2(x)
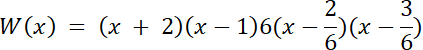
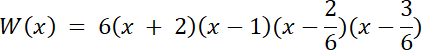
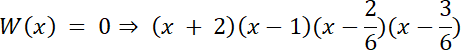
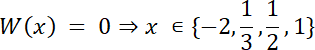

Skorzystaj z twierdzenia 2, o wymiernych pierwiastkach wielomianu, o współczynnikach całkowitych, wyznać jeden z pierwiastków, a następnie z równania 3 stopnia kolejny pierwiastek (o ile istnieje). Ze schematu Hornera wyznacz trójmian kwadratowy, który jest dzielnikiem wielomianu W(x), a z niego miejsca zerowe, aby określić czy pierwiastki wielomianu są wymierne.

Zadanie 1.
264Zadanie 2.
264Zadanie 3.
265Zadanie 4.
265Zadanie 5.
265Zadanie 7.
265Zadanie 10.
265Ćwiczenie 1.
266Ćwiczenie 2.
267Zadanie 1.
269Zadanie 2.
269Zadanie 3.
269Zadanie 4.
269Zadanie 5.
269Zadanie 6.
269Zadanie 7.
269Zadanie 8.
269Zadanie 9.
269Zadanie 1.
272Zadanie 2.
272Zadanie 3.
272Zadanie 4.
272Zadanie 5.
272Zadanie 6.
272Zadanie 7.
272Ćwiczenie 3.
274Ćwiczenie 4.
274Ćwiczenie 6.
276Ćwiczenie 7.
277Zadanie 1.
277Zadanie 2.
278Zadanie 3.
278Zadanie 4.
278Zadanie 5.
278Zadanie 6.
278Zadanie 7.
278Zadanie 8.
278Zadanie 9.
278Zadanie 1.
283Zadanie 3.
283Zadanie 4.
284Zadanie 5.
284Zadanie 13.
284Ćwiczenie 4.
286Zadanie 1.
290Zadanie 2.
290Zadanie 3.
290Zadanie 4.
290Zadanie 5.
290Zadanie 6.
290Ćwiczenie 4.
294Zadanie 1.
295Zadanie 2.
296Zadanie 3.
296Zadanie 4.
296Zadanie 5.
296Zadanie 6.
296Zadanie 7.
296Zadanie 8.
296Zadanie 9.
296Zadanie 10.
296Zadanie 1.
301Zadanie 2.
301Zadanie 3.
301Zadanie 6.
302Zadanie 7.
302Zadanie 9.
302Zadanie 11.
302Zadanie 12.
302Zadanie 13.
302Ćwiczenie 2.
304Ćwiczenie 3.
305Zadanie 1.
306Zadanie 2.
306Zadanie 3.
307Zadanie 4.
307Zadanie 5.
307Zadanie 6.
307Zadanie 7.
307Zadanie 8.
307Zadanie 9.
307Zadanie 10.
307Ćwiczenie 1.
308Zadanie 1.
310Zadanie 2.
310Zadanie 3.
311Zadanie 4.
311Zadanie 5.
311Zadanie 6.
311Zadanie 7.
311Zadanie 8.
311Zadanie 9.
311Zadanie 10.
311Zadanie 17.
315Zadanie 18.
315Zadanie 24.
315Zadanie 26.
315Zadanie 28.
315
