W tym zadaniu sprawdzić, czy istnieją takie liczby a, b, dla których zachodzi równość wielomianowa: W(x)∙F(x) = H(x),
W(x)∙F(x) = (x–2)2(x–2),∙(ax + b)
W(x)∙F(x) = (x2–4x + 4) (x–2)(ax + b)
W(x)∙F(x) = (x3–2x2–4x2 + 8x + 4x–8)(ax + b)
W(x)∙F(x) = (x3–6x2 + 12x–8) (ax + b)
W(x)∙F(x) = ax4 + bx3–6ax3–6bx2 + 12ax2 + 12bx–8ax–8b
W(x)∙F(x) = ax4 + (b–6a)x3 + (–6b + 12a)x2 + (12b–8a)x–8b
W(x)∙F(x) = H(x), więc:
ax4 + (b–6a)x3 + (–6b–4a)x2 + (–4b–8a)x–8b = x4–5x3 + 6x2 + 4x–8
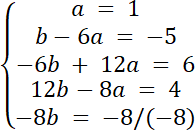
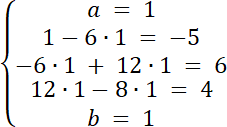
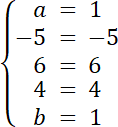
więc: a = 1 ∧ b = 1

Na początku, wyznacz iloczyn wielomianów W(x)∙F(x) i zapisz go w postaci ogólnej, a następnie przyrównaj wynik iloczynu, z wielomianem H(x): W(x)∙F(x) = H(x), a następnie przyrównaj współczynniki odpowiednich potęg do siebie. Wielomiany są równe, wtedy i tylko wtedy, gdy wszystkie współczynniki przy odpowiednich potęgach są sobie równe.

Zadanie 1.
264Zadanie 2.
264Zadanie 3.
265Zadanie 4.
265Zadanie 5.
265Zadanie 7.
265Zadanie 10.
265Ćwiczenie 1.
266Ćwiczenie 2.
267Zadanie 1.
269Zadanie 2.
269Zadanie 3.
269Zadanie 4.
269Zadanie 5.
269Zadanie 6.
269Zadanie 7.
269Zadanie 8.
269Zadanie 9.
269Zadanie 1.
272Zadanie 2.
272Zadanie 3.
272Zadanie 4.
272Zadanie 5.
272Zadanie 6.
272Zadanie 7.
272Ćwiczenie 3.
274Ćwiczenie 4.
274Ćwiczenie 6.
276Ćwiczenie 7.
277Zadanie 1.
277Zadanie 2.
278Zadanie 3.
278Zadanie 4.
278Zadanie 5.
278Zadanie 6.
278Zadanie 7.
278Zadanie 8.
278Zadanie 9.
278Zadanie 1.
283Zadanie 3.
283Zadanie 4.
284Zadanie 5.
284Zadanie 13.
284Ćwiczenie 4.
286Zadanie 1.
290Zadanie 2.
290Zadanie 3.
290Zadanie 4.
290Zadanie 5.
290Zadanie 6.
290Ćwiczenie 4.
294Zadanie 1.
295Zadanie 2.
296Zadanie 3.
296Zadanie 4.
296Zadanie 5.
296Zadanie 6.
296Zadanie 7.
296Zadanie 8.
296Zadanie 9.
296Zadanie 10.
296Zadanie 1.
301Zadanie 2.
301Zadanie 3.
301Zadanie 6.
302Zadanie 7.
302Zadanie 9.
302Zadanie 11.
302Zadanie 12.
302Zadanie 13.
302Ćwiczenie 2.
304Ćwiczenie 3.
305Zadanie 1.
306Zadanie 2.
306Zadanie 3.
307Zadanie 4.
307Zadanie 5.
307Zadanie 6.
307Zadanie 7.
307Zadanie 8.
307Zadanie 9.
307Zadanie 10.
307Ćwiczenie 1.
308Zadanie 1.
310Zadanie 2.
310Zadanie 3.
311Zadanie 4.
311Zadanie 5.
311Zadanie 6.
311Zadanie 7.
311Zadanie 8.
311Zadanie 9.
311Zadanie 10.
311Zadanie 17.
315Zadanie 18.
315Zadanie 24.
315Zadanie 26.
315Zadanie 28.
315
