Prosto do matury 3. Podręcznik do matematyki dla liceum ogólnokształcącego i technikum. Zakres podstawowy

Podręcznik, Wydawnictwo: Nowa Era

Zadanie 23. - strona 38

Oblicz kąty trójkąta ABC oraz pole P koła opisanego na tym trójkącie, jeśli w trójkącie rozwartokątnym ABC o kącie rozwartym przy wierzchołku B dane są $\text{[math]}$ i $\text{[math]}$ . Poprowadzono wysokość BD i otrzymano trójkąt równoramienny ABD.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

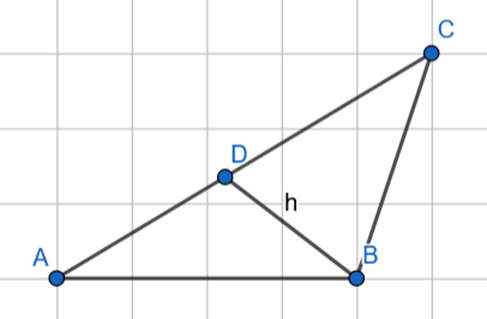
Trójkąt ABD jest równoramienny prostokątny, więc:

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

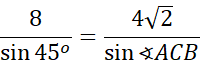
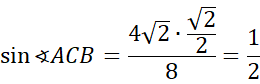
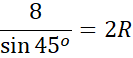
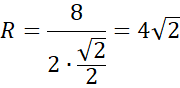
Dwukrotnie skorzystaj z twierdzenia Pitagorasa, aby wyznaczyć brakujące długości boków podanego trójkąta. Następnie skorzystaj z twierdzenia sinusów $\text{[math]}$ , gdzie $\text{[math]}$ to boki trójkąta, $\text{[math]}$ to kąty odpowiednio przeciwległe do tych boków, a $\text{[math]}$ to długość promienia okręgu opisanego na tym trójkącie i z wyznacz miarę kąta ACB, a następnie kąta ABC. Na koniec wyznacz długość promienia okręgu opisanego na tym trójkącie i jego pole.

Zadanie 4.13., strona 105, Matematyka. Klasa 3. Zbiór zadań. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 5.6, strona 47, Prosto do matury. Matematyka. Klasa 1. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 6., strona 28, Matematyka. Klasa 7. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie co umiem? 1, strona 39, Matematyka. Klasa 6. Podręcznik - rozwiązania i odpowiedzi

Zadanie do samodzielnego rozwiązania 2., strona 27, Matematyka. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Zadanie 7., strona 36, Matematyka wokół nas. Klasa 5. Zeszyt ćwiczeń. Część 2 - rozwiązania i odpowiedzi

Zadanie 77., strona 53, Matematyka z plusem. Klasa 2. Zbiór zadań. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Zadanie 19., strona 141, Matematyka. Klasa 2. Zakres podstawowy. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 7, strona 27, Matematyka. Klasa 5. Podręcznik – rozwiązania i odpowiedzi

Ćwiczenie 5., strona 87, Matematyka. Klasa 5. Zeszyt ćwiczeń. Część 2 - rozwiązania i odpowiedzi

Zadanie 1.1.

10

10

10

10

10

Zadanie 1.2.

10

10

10

10

10

Zadanie 1.3.

10

10

10

10

10

10

11

Zadanie 1.8.

11

11

11

11

11

Zadanie 1.9.

11

11

11

11

11

11

11

Zadanie 1.10.

11

11

11

11

Zadanie 1.12.

11

11

11

11

11

Zadanie 1.13.

11

11

11

11

11

11

11

11

18

Zadanie 2.2.

18

18

18

18

18

18

Zadanie 2.4.

18

18

18

18

18

18

18

18

Zadanie 2.9.

19

19

19

19

19

19

19

19

19

19

19

19

Zadanie 2.19.

19

19

19

19

20

20

20

20

20

20

20

20

Zadanie 3.1.

24

24

24

24

24

24

24

24

Zadanie 3.5.

24

24

24

24

24

Zadanie 3.6.

24

24

24

24

24

24

25

25

25

Zadanie 3.11.

25

25

25

25

25

25

25

25

25

25

25

25

25

26

26

26

26

26

26

26

26

26

26

32

32

33

33

33

Zadanie 4.6.

33

33

33

33

33

33

33

33

33

33

33

33

33

34

34

34

Zadanie 4.18.

34

34

34

Zadanie 4.19.

34

34

34

34

34

34

34

34

34

35

35

35

35

35

35

35

35

36

36

36

36

36

36

36

36

36

37

37

37

37

37

37

37

37

37

38

38

38

Zadanie 22.

38

38

38

38

38

38

38

Zadanie 27.

38

38

38

38

38

38

Pełny spis treści