Oblicz (z dokładnością do drugiego miejsca po przecinku) stosunek promienia okręgu opisanego na tym trójkącie do promienia okręgu wpisanego w ten trójkąt, jeśli kąt między ramionami trójkąta równoramiennego ma miarę
.
– ramiona trójkąta
– podstawa trójkąta
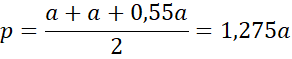
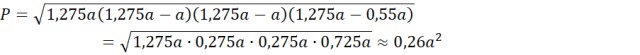
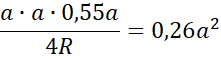
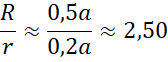
Skorzystaj z twierdzenia cosinusów:
, gdzie
to boki trójkąta, a
to kąt leżacy naprzeciwko boku
i na tej podstawie oblicz długość brakującego boku w podanym trójkącie.
Następnie skorzystaj ze wzoru Herona na pole trójkąta:
, gdzie
to połowa obwodu, a
to boki trójkąta. Następnie skorzystaj ze wzorów na pole trójkąta z promieniami opisanym:
oraz wpisanym:
w trójkąt, wyznacz ich długości, a następnie stosunek promienia okręgu opisanego do promienia okręgu wpisanego.