Udowodnij, że pole tego trójkąta nie jest większe niż sinus dowolnego jego kąta, jeśli w kwadracie o boku długości 1 zawarty jest trójkąt.
![]() – przekątna kwadratu i najdłuższy bok trójkąta
– przekątna kwadratu i najdłuższy bok trójkąta
![]() – kąty ostre trójkąta
– kąty ostre trójkąta
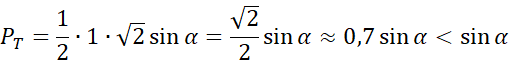
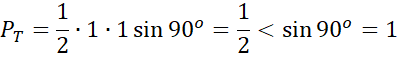
Pole trójkąta nie jest większe niż sinus jego dowolnego kąta.
To kończy dowód.


Zadanie 1.1.
10Zadanie 1.2.
10Zadanie 1.3.
10Zadanie 1.8.
11Zadanie 1.9.
11Zadanie 1.10.
11Zadanie 1.12.
11Zadanie 1.13.
11Zadanie 2.2.
18Zadanie 2.4.
18Zadanie 2.9.
19Zadanie 2.19.
19Zadanie 3.1.
24Zadanie 3.5.
24Zadanie 3.6.
24Zadanie 3.11.
25Zadanie 4.6.
33Zadanie 4.18.
34Zadanie 4.19.
34Zadanie 22.
38Zadanie 27.
38
