Udowodnij, że nie istnieje trójkąt, w którym sinusy kątów są równe
![]() i
i
![]() .
.
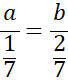
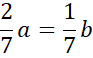
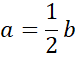
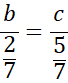
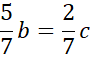
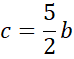
![]()
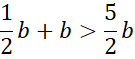
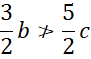
Nierówność trójkąta nie jest spełniona, więc nie istnieje trójkąt o takich sinusach kątów.
To kończy dowód.

Skorzystaj z twierdzenia sinusów
![]() , gdzie
, gdzie
![]() to boki trójkąta,
to boki trójkąta,
![]() to kąty odpowiednio przeciwległe do tych boków, a
to kąty odpowiednio przeciwległe do tych boków, a
![]() to długość promienia okręgu opisanego na tym trójkącie i z powstałych równań wyznacz długość boków
to długość promienia okręgu opisanego na tym trójkącie i z powstałych równań wyznacz długość boków
![]() i
i
![]() w zależności od długości boku
w zależności od długości boku
![]() . Następnie skorzystaj z nierówności trójkąta – suma długości dwóch krótszych boków musi być większa od najdłuższego i sprawdź, czy jest ona spełniona.
. Następnie skorzystaj z nierówności trójkąta – suma długości dwóch krótszych boków musi być większa od najdłuższego i sprawdź, czy jest ona spełniona.

Zadanie 1.1.
10Zadanie 1.2.
10Zadanie 1.3.
10Zadanie 1.8.
11Zadanie 1.9.
11Zadanie 1.10.
11Zadanie 1.12.
11Zadanie 1.13.
11Zadanie 2.2.
18Zadanie 2.4.
18Zadanie 2.9.
19Zadanie 2.19.
19Zadanie 3.1.
24Zadanie 3.5.
24Zadanie 3.6.
24Zadanie 3.11.
25Zadanie 4.6.
33Zadanie 4.18.
34Zadanie 4.19.
34Zadanie 22.
38Zadanie 27.
38
