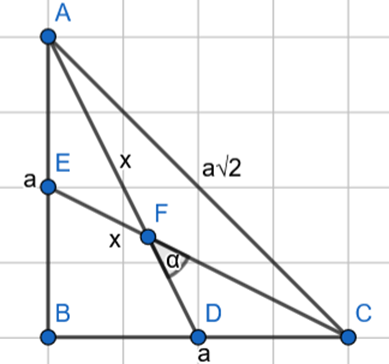
Udowodnij, że w równoramiennym trójkącie prostokątnym tangens kąta ostrego między środkowymi poprowdzonymi z wierzchołków kątów ostrych jest równy 0,75.
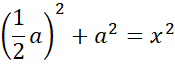
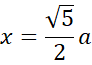
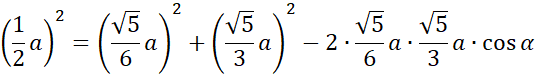
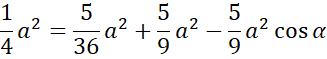
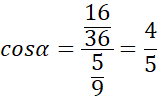
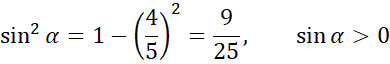
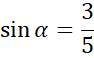
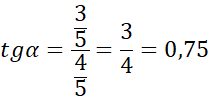
To kończy dowód.

Skorzystaj z twierdzenia Pitagorasa, aby wyznaczyć długość środkowej, a następnie z twierdzenia cosinusów:
![]() , gdzie
, gdzie
![]() to boki trójkąta, a
to boki trójkąta, a
![]() to kąt leżacy naprzeciwko boku
to kąt leżacy naprzeciwko boku
![]() i na tej podstawie oblicz cosinus podanego kąta - skorzystaj z tego, że przecięcie środkowych dzieli je w stosunku 2:1. Na koniec korzystając z jedynki trygonometrycznej oblicz sinus podanego kąta oraz jego tangens.
i na tej podstawie oblicz cosinus podanego kąta - skorzystaj z tego, że przecięcie środkowych dzieli je w stosunku 2:1. Na koniec korzystając z jedynki trygonometrycznej oblicz sinus podanego kąta oraz jego tangens.

Zadanie 1.1.
10Zadanie 1.2.
10Zadanie 1.3.
10Zadanie 1.8.
11Zadanie 1.9.
11Zadanie 1.10.
11Zadanie 1.12.
11Zadanie 1.13.
11Zadanie 2.2.
18Zadanie 2.4.
18Zadanie 2.9.
19Zadanie 2.19.
19Zadanie 3.1.
24Zadanie 3.5.
24Zadanie 3.6.
24Zadanie 3.11.
25Zadanie 4.6.
33Zadanie 4.18.
34Zadanie 4.19.
34Zadanie 22.
38Zadanie 27.
38
