Wyznacz długości odcinków, na które dwusieczna kąta przy podstawie dzieli ramię tego trójkąta, jeśli dany jest trójkąt równoramienny ABC, w którym
i
.
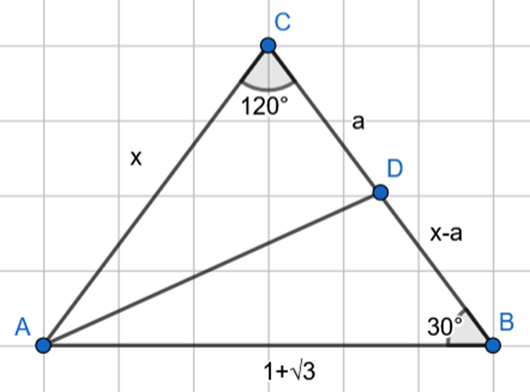
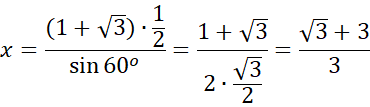
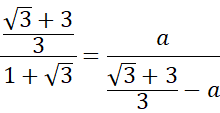
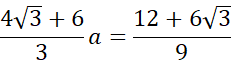
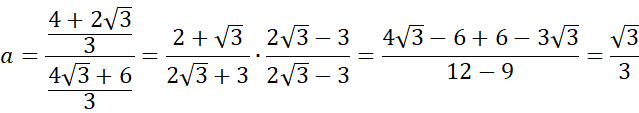
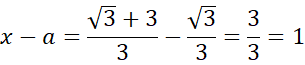
Skorzystaj z twierdzenia sinusów
, gdzie
to boki trójkąta,
to kąty odpowiednio przeciwległe do tych boków, a
to długość promienia okręgu opisanego na tym trójkącie i na tej podstawie wyznacz długość ramienia trójkąta.
Następnie skorzystaj z twierdzenia o dwusiecznej:
, gdzie
to odcinki na jakie dwusieczna dzieli bok trójkąta, a
to jego pozostałe boki i na tej podstawie wyznacz długości odcinków, na które dwusieczna kąta przy podstawie dzieli ramię tego trójkąta.