Udowodnij, że pole trójkąta o kątach
wpisanego w okrąg o promieniu R wyraża się wzorem
.
– boki trójkąta
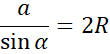
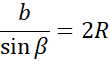
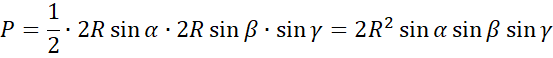
To kończy dowód.
Skorzystaj z twierdzenia sinusów
, gdzie
to boki trójkąta,
to kąty odpowiednio przeciwległe do tych boków, a
to długość promienia okręgu opisanego na tym trójkącie i na tej podstawie oblicz długości boków
i
, a następnie pod wzór na pole trójkąta z sinusem:
, gdzie
to sąsiednie boki trójkąta, a
to kąt między nimi, podstaw znane wartości i je oblicz.