W tym zadaniu musisz rozwiązać układ równań
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Zatem:
![]()
![]()
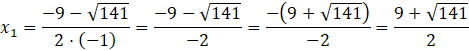
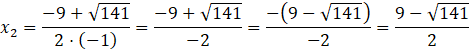
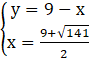 lub
lub
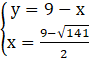
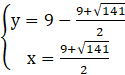 lub
lub
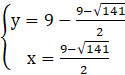
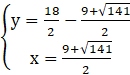 lub
lub
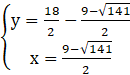
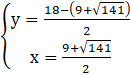 lub
lub
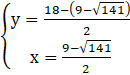
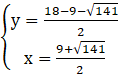 lub
lub
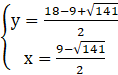
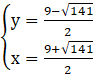 lub
lub
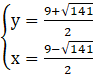

Rozwiążmy układ równań metodą podstawiania. Z pierwszego równania wyznaczamy y:
![]()
![]()
Korzystając z równości
![]() w drugim równaniu, w miejsce y podstawiamy
w drugim równaniu, w miejsce y podstawiamy
![]() :
:
![]()
![]()
![]()
![]()
Rozwiązujemy drugie równanie z układu równań. Równanie
![]() jest w postaci
jest w postaci
![]() , więc możemy policzyć jego rozwiązania za pomocą wyróżnika równania kwadratowego
, więc możemy policzyć jego rozwiązania za pomocą wyróżnika równania kwadratowego
![]() , który jest określony wzorem
, który jest określony wzorem
![]() .
.
Jeżeli
![]() , to równanie ma dwa rozwiązania:
, to równanie ma dwa rozwiązania:
![]()
![]()
Jeżeli
![]() , to równanie ma jedno rozwiązanie:
, to równanie ma jedno rozwiązanie:
![]()
Jeżeli
![]() , to równanie nie ma rozwiązań.
, to równanie nie ma rozwiązań.
Współczynniki liczbowe równania
![]() to:
to:
![]()
![]()
![]()
Zatem:
![]()
![]() , więc równanie ma dwa rozwiązania:
, więc równanie ma dwa rozwiązania:
![]()
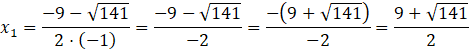
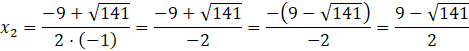
![]()
![]()
Podstawiamy wyznaczone wartości x do układu i obliczamy y:
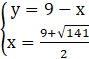 lub
lub
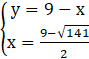
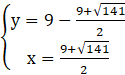 lub
lub
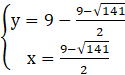
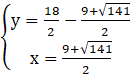 lub
lub
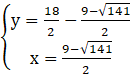
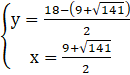 lub
lub
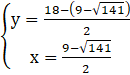
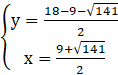 lub
lub
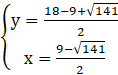
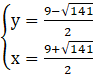 lub
lub
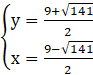

Ćwiczenie A.
186Ćwiczenie C.
187Przykład 1.
187Przykład 2.
188Zadanie 1.
188Zadanie 3.
189Zadanie 4.
189Ćwiczenie A.
190Ćwiczenie B.
29Przykład 2.
192Zadanie 1.
193Zadanie 2.
193Zadanie 3.
193Zadanie 4.
193Zadanie 5.
193Zadanie 6.
193Zadanie 7.
193Zadanie 8.
193Zadanie 9.
194Zadanie 14.
194Ćwiczenie A.
196Przykład 1.
197Przykład 2.
197Zadanie 1.
198Zadanie 4.
198Zadanie 5.
199Zadanie 6.
199Zadanie 8.
199Zadanie 10.
199Zadanie 1.
200Zadanie 2.
200Zadanie 3.
200Zadanie 4.
200Zadanie 8.
200Zadanie 9.
200Zadanie 10.
200Zadanie 11.
200
