Sprawdzamy po kolei, które równania mają dwa rozwiązania, obliczając ich deltę.
![]()
![]()
![]()
![]()
Zatem:
![]()
Równanie
![]() ma dwa rozwiązania.
ma dwa rozwiązania.
![]()
![]()
![]()
![]()
Zatem:
![]()
Równanie
![]() ma dwa rozwiązania.
ma dwa rozwiązania.
![]()
![]()
![]()
![]()
Zatem:
![]()
Równanie
![]() ma dwa rozwiązania.
ma dwa rozwiązania.
![]()
![]()
![]()
![]()
Zatem:
![]()
Równanie
![]() ma dwa rozwiązania.
ma dwa rozwiązania.
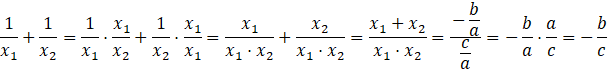
Suma odwrotności rozwiązań równania
![]() :
:
![]()
Suma odwrotności rozwiązań równania
![]() :
:
![]()
Suma odwrotności rozwiązań równania
![]() :
:
![]()
Suma odwrotności rozwiązań równania
![]() :
:
![]()
![]() , więc równanie
, więc równanie
![]() ma największą sumę odwrotności jego rozwiązań.
ma największą sumę odwrotności jego rozwiązań.
Odp. C.
![]()

Sprawdzamy po kolei, które równania mają dwa rozwiązania, obliczając ich deltę.
Współczynniki liczbowe równania
![]() to:
to:
![]()
![]()
![]()
Zatem:
![]()
![]() , więc równanie
, więc równanie
![]() ma dwa rozwiązania.
ma dwa rozwiązania.
Współczynniki liczbowe równania
![]() to:
to:
![]()
![]()
![]()
Zatem:
![]()
![]() , więc równanie
, więc równanie
![]() ma dwa rozwiązania.
ma dwa rozwiązania.
Współczynniki liczbowe równania
![]() to:
to:
![]()
![]()
![]()
Zatem:
![]()
![]() , więc równanie
, więc równanie
![]() ma dwa rozwiązania.
ma dwa rozwiązania.
Współczynniki liczbowe równania
![]() to:
to:
![]()
![]()
![]()
Zatem:
![]()
![]() , więc równanie
, więc równanie
![]() ma dwa rozwiązania.
ma dwa rozwiązania.
Ze wzorów Viete’a wiemy, że jeśli równanie kwadratowe
![]() , gdzie
, gdzie
![]() , ma dwa rozwiązania
, ma dwa rozwiązania
![]() i
i
![]() , to:
, to:
![]()
![]()
Zapiszmy wzór na sumę odwrotności rozwiązań, korzystając ze wzorów Viete’a:
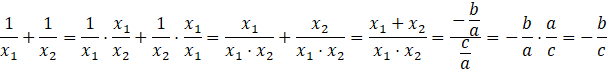
Skoro każde równanie ma dwa rozwiązania, to obliczmy sumę odwrotności tych rozwiązań, korzystając z wyżej wyznaczonego wzoru.
Suma odwrotności rozwiązań równania
![]() :
:
![]()
Suma odwrotności rozwiązań równania
![]() :
:
![]()
Suma odwrotności rozwiązań równania
![]() :
:
![]()
Suma odwrotności rozwiązań równania
![]() :
:
![]()
![]() , więc równanie
, więc równanie
![]() ma największą sumę odwrotności jego rozwiązań.
ma największą sumę odwrotności jego rozwiązań.