W tym zadaniu musisz obliczyć sumę kwadratów rozwiązań równania
![]() , korzystając ze wzorów Viete’a.
, korzystając ze wzorów Viete’a.
![]()
![]()
![]()
![]()
Zatem:
![]()
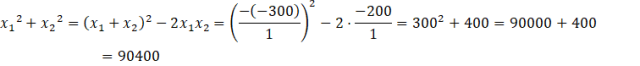
Suma kwadratów rozwiązań równania
![]() wynosi
wynosi
![]() .
.

Najpierw sprawdzamy, czy równanie
![]() ma dwa rozwiązania, obliczając jego deltę.
ma dwa rozwiązania, obliczając jego deltę.
Współczynniki liczbowe równania
![]() to:
to:
![]()
![]()
![]()
Zatem:
![]()
![]() , więc równanie ma dwa rozwiązania.
, więc równanie ma dwa rozwiązania.
Ze wzorów Viete’a wiemy, że jeśli równanie kwadratowe
![]() , gdzie
, gdzie
![]() , ma dwa rozwiązania
, ma dwa rozwiązania
![]() i
i
![]() , to:
, to:
![]()
![]()
Zapisujemy sumę kwadratów rozwiązań w takiej postaci, aby dało się w niej zastosować wzory Viete’a:
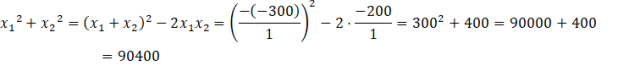
Sumę
![]() możemy zapisać jako
możemy zapisać jako
![]() , ponieważ:
, ponieważ:
![]()

Ćwiczenie A.
186Ćwiczenie C.
187Przykład 1.
187Przykład 2.
188Zadanie 1.
188Zadanie 3.
189Zadanie 4.
189Ćwiczenie A.
190Ćwiczenie B.
29Przykład 2.
192Zadanie 1.
193Zadanie 2.
193Zadanie 3.
193Zadanie 4.
193Zadanie 5.
193Zadanie 6.
193Zadanie 7.
193Zadanie 8.
193Zadanie 9.
194Zadanie 14.
194Ćwiczenie A.
196Przykład 1.
197Przykład 2.
197Zadanie 1.
198Zadanie 4.
198Zadanie 5.
199Zadanie 6.
199Zadanie 8.
199Zadanie 10.
199Zadanie 1.
200Zadanie 2.
200Zadanie 3.
200Zadanie 4.
200Zadanie 8.
200Zadanie 9.
200Zadanie 10.
200Zadanie 11.
200
