Oblicz prędkość satelity, z jaką okrąża Ziemię, znajdując się 1000 km nad powierzchnią Ziemi. Określ również kierunek przemieszczenia się na niebie satelity z punktu widzenia obserwatora.
Prędkość w ruchu obrotowym:
![]()
Masa Ziemi:
![]()
Promień równikowy Ziemi:
![]()
Wysokość:
![]()
Odległość od środka Ziemi do satelity:
![]()
Skoro satelita krąży wokół Ziemi swobodnie, to siła grawitacji jest równa sile dośrodkowej.
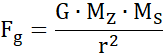
Siła dośrodkowa:
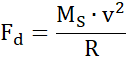
![]()
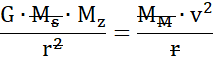

Prędkość, jaką należy nadać satelicie (bez wpływu ruchu obrotowego):
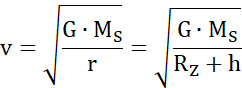
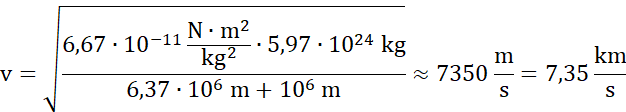
Satelita porusza się z zachodu na wschód, dlatego prędkość liniowa w ruchu obrotowym będzie przyspieszać satelitę, a nie spowalniać.
![]()
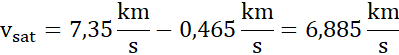
Satelita będzie poruszać się z zachodu na wschód względem nieruchomego obserwatora.

Wykorzystaj wzór na siłę przyciągania grawitacyjnego między dwoma ciałami:
![]()
gdzie F – siła grawitacji [N],
G – stała grawitacji [![]()
M1 – masa pierwszego ciała [kg],
M2 – masa drugiego ciała [kg],
r – odległość między środkami dwóch ciał [m].
Wzór na siłę dośrodkową ma postać:
![]()
gdzie Fo – siła dośrodkowa [N],
m – masa ciała [kg],
v – prędkość ciała [![]()
R – promień, wokół którego obraca się ciało [m].
Ziemia obraca się z zachodu na wschód, dlatego prędkość związana z ruchem obrotowym pomaga nam wprowadzić satelitę na orbitę.

Zadanie 11.1.8.
16Zadanie 11.1.9.
17Zadanie 11.1.10.
17Zadanie 11.2.2.
21Zadanie 11.2.7.
25Zadanie 11.3.14.
33Zadanie 11.3.17.
34Zadanie 11.3.19.
35Zadanie 11.3.20.
35Zadanie 11.3.22.
35Zadanie 11.3.24.
36Zadanie 11.3.25.
36Zadanie 11.3.26.
36Zadanie 11.4.10.
44Zadanie 11.4.11.
44Zadanie 11.4.12.
44Zadanie 11.4.20.
46Zadanie 11.4.22.
46Zadanie 11.5.8.
54Zadanie 11.5.16.
57Zadanie 11.6.1.
66Zadanie 11.6.6.
67Zadanie 11.6.7.
67Zadanie 11.6.11.
68Zadanie 11.6.12.
69Zadanie 11.6.16.
69Zadanie 11.6.22.
70Zadanie 11.6.23.
71Zadanie 11.6.24.
71Zadanie 11.6.25.
71Zadanie 11.6.26.
72Zadanie 11.7.1.
74Zadanie 11.7.3.
75Zadanie 11.7.4.
75
