Policz, ile wynosi masa układu Syriusz oraz masa każdej z gwiazd, które tworzą układ przedstawiony na rysunku.
Średnia odległość:
![]()
Okres:
![]()
![]()
Zgodnie ze wzorem wynikającym z 3 prawa Keplera:
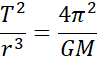
![]()
Masa układu:
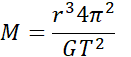
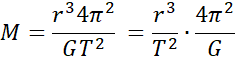
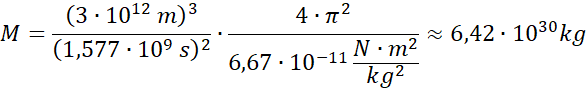
Masa ciała A i B jest równa masie układu:
![]()
Ciała poruszają się z siłami dośrodkowymi o takich samych prędkościach kątowych:
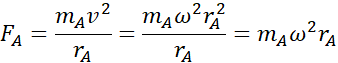
![]()
Z zależności na siłę grawitacji:
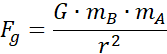
Jest ona równa siłom dośrodkowym:
![]()
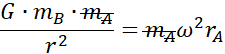
Promień rA:
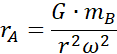
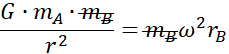
Promień rB:
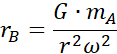
Porównanie promieni:
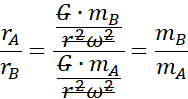
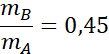
![]()
![]()
![]()
Masa ciała mA:
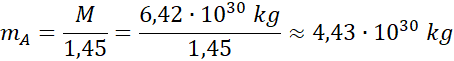
![]()
![]()

Wzór na siłę odśrodkową ma postać:
![]()
gdzie Fo – siła odśrodkowa [N],
m – masa ciała [kg],
v – prędkość ciała [![]()
R – promień [m]
Wzór na prędkość w ruchu obrotowym:
![]()
gdzie ![]()
![]()
Wykorzystaj wzór na siłę przyciągania grawitacyjnego między dwoma ciałami:
![]()
gdzie F – siła grawitacji [N],
G – stała grawitacji [![]()
M1 – masa pierwszego ciała [kg],
M2 – masa drugiego ciała [kg],
r – odległość między środkami dwóch ciał [m].

Zadanie 11.1.8.
16Zadanie 11.1.9.
17Zadanie 11.1.10.
17Zadanie 11.2.2.
21Zadanie 11.2.7.
25Zadanie 11.3.14.
33Zadanie 11.3.17.
34Zadanie 11.3.19.
35Zadanie 11.3.20.
35Zadanie 11.3.22.
35Zadanie 11.3.24.
36Zadanie 11.3.25.
36Zadanie 11.3.26.
36Zadanie 11.4.10.
44Zadanie 11.4.11.
44Zadanie 11.4.12.
44Zadanie 11.4.20.
46Zadanie 11.4.22.
46Zadanie 11.5.8.
54Zadanie 11.5.16.
57Zadanie 11.6.1.
66Zadanie 11.6.6.
67Zadanie 11.6.7.
67Zadanie 11.6.11.
68Zadanie 11.6.12.
69Zadanie 11.6.16.
69Zadanie 11.6.22.
70Zadanie 11.6.23.
71Zadanie 11.6.24.
71Zadanie 11.6.25.
71Zadanie 11.6.26.
72Zadanie 11.7.1.
74Zadanie 11.7.3.
75Zadanie 11.7.4.
75
