Policz, o ile wzrośnie prędkość satelity w punkcie A, aby była w stanie przejść z orbity kołowej na eliptyczną.
Prędkość w punkcie A (orbita kołowa):
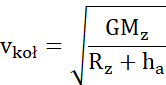
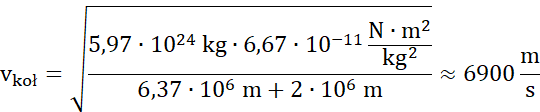
Kiedy satelita wejdzie na orbitę eliptyczną, to punkt A będzie w perygeum.
Z zasady zachowania momentu pędu:
![]()
![]()
αp – kąt między promieniem wodzącym a wektorem prędkości w perysferze,
αa –kąt między promieniem wodzącym a wektorem prędkości w apogeum,
rp – odległość od perysfery do Ziemi,
ra – odległość od perysfery do Ziemi,
![]()
![]()
![]()
![]()
![]()
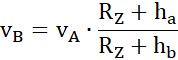
Z zasady zachowania energii:
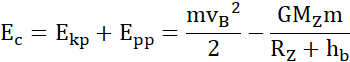
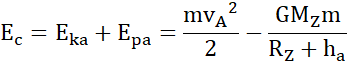
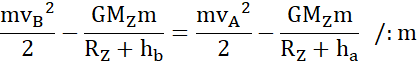
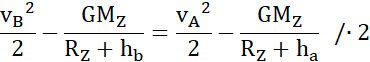
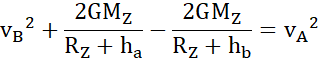
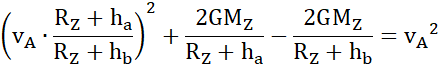
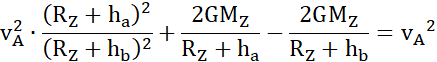
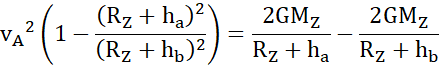

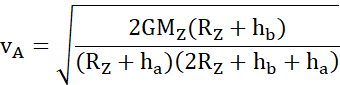
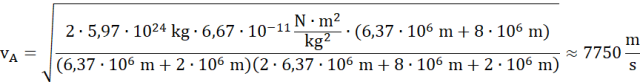
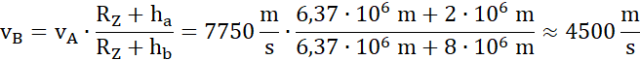
O ile musi wzrosnąć prędkość
![]()

Wzór na prędkość satelity krążącej po orbicie kołowej ma postać:
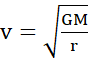
Gdzie v – prędkość satelity [![]()
M – masa planety [kg],
G – stała grawitacji [![]()
r – promień orbity [m].
Moment pędu obliczysz ze wzoru:
![]()
gdzie L – moment pędu [![]()
m – masa ciała [kg],
v – prędkość ciała [![]()
r – promień wodzący [m],
α – kąt między promieniem wodzącym a wektorem prędkości.
Perygeum to miejsce, w którym znajduje się ciało niebieskie, kiedy znajduje się najbliżej Ziemi.
Apogeum to miejsce, w którym znajduje się ciało niebieskie, kiedy znajduje się najdalej od Ziemi.
Zasada zachowania energii mówi nam, że całkowita energia w układzie nie ulega zmianie.
Energia całkowita to suma energii potencjalnej i kinetycznej w danym punkcie.

Zadanie 11.1.8.
16Zadanie 11.1.9.
17Zadanie 11.1.10.
17Zadanie 11.2.2.
21Zadanie 11.2.7.
25Zadanie 11.3.14.
33Zadanie 11.3.17.
34Zadanie 11.3.19.
35Zadanie 11.3.20.
35Zadanie 11.3.22.
35Zadanie 11.3.24.
36Zadanie 11.3.25.
36Zadanie 11.3.26.
36Zadanie 11.4.10.
44Zadanie 11.4.11.
44Zadanie 11.4.12.
44Zadanie 11.4.20.
46Zadanie 11.4.22.
46Zadanie 11.5.8.
54Zadanie 11.5.16.
57Zadanie 11.6.1.
66Zadanie 11.6.6.
67Zadanie 11.6.7.
67Zadanie 11.6.11.
68Zadanie 11.6.12.
69Zadanie 11.6.16.
69Zadanie 11.6.22.
70Zadanie 11.6.23.
71Zadanie 11.6.24.
71Zadanie 11.6.25.
71Zadanie 11.6.26.
72Zadanie 11.7.1.
74Zadanie 11.7.3.
75Zadanie 11.7.4.
75
