Policz masy gwiazd oraz ich stosunek energii kinetycznych, jeśli poruszają się po orbitach kołowych w układzie podwójnym.
Energia kinetyczna każdego ciała:
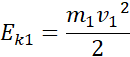
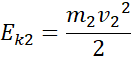
![]()
Siła odśrodkowa jest równa sile grawitacji:
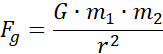
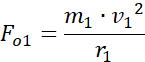
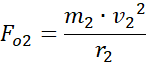
![]()
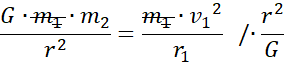
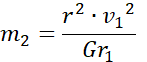
![]()
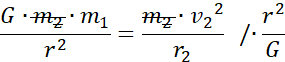
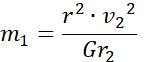
Prędkość liniowa:
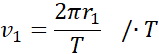
![]()
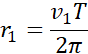
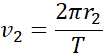
Z tego mamy:
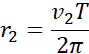
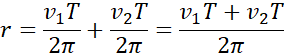
Masa:
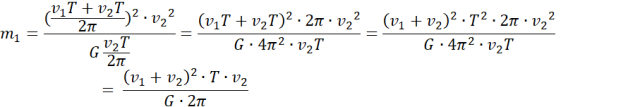
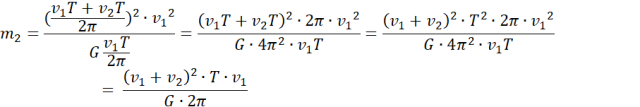
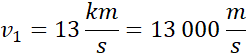
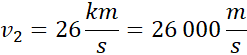
![]()
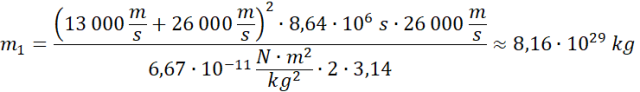

Energie kinetyczne:
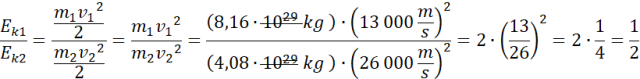

Wzór na siłę odśrodkową ma postać:
![]()
gdzie Fo – siła odśrodkowa [N],
m – masa ciała [kg],
v – prędkość ciała [![]()
R – promień [m]
Wykorzystaj wzór na siłę przyciągania grawitacyjnego między dwoma ciałami:
![]()
gdzie F – siła grawitacji [N],
G – stała grawitacji [![]()
M1 – masa pierwszego ciała [kg],
M2 – masa drugiego ciała [kg],
r – odległość między środkami dwóch ciał [m].
Wzór na energię kinetyczną:
![]()
Ek – energia kinetyczna [J],
m – masa ciała [kg],
Gdzie v – prędkość ciała [![]()
Wzór na prędkość w ruchu obrotowym:
![]()
gdzie T – okres obrotu [s].
v – prędkość ciała [![]()
R – promień, wokół którego obraca się ciało [m].

Zadanie 11.1.8.
16Zadanie 11.1.9.
17Zadanie 11.1.10.
17Zadanie 11.2.2.
21Zadanie 11.2.7.
25Zadanie 11.3.14.
33Zadanie 11.3.17.
34Zadanie 11.3.19.
35Zadanie 11.3.20.
35Zadanie 11.3.22.
35Zadanie 11.3.24.
36Zadanie 11.3.25.
36Zadanie 11.3.26.
36Zadanie 11.4.10.
44Zadanie 11.4.11.
44Zadanie 11.4.12.
44Zadanie 11.4.20.
46Zadanie 11.4.22.
46Zadanie 11.5.8.
54Zadanie 11.5.16.
57Zadanie 11.6.1.
66Zadanie 11.6.6.
67Zadanie 11.6.7.
67Zadanie 11.6.11.
68Zadanie 11.6.12.
69Zadanie 11.6.16.
69Zadanie 11.6.22.
70Zadanie 11.6.23.
71Zadanie 11.6.24.
71Zadanie 11.6.25.
71Zadanie 11.6.26.
72Zadanie 11.7.1.
74Zadanie 11.7.3.
75Zadanie 11.7.4.
75
