Policz zmianę prędkości modułu, kiedy przeszedł z peryselenium z orbity eliptycznej na orbitę kołową na wysokości h1.
Promień orbity kołowej:
![]()
Prędkość na orbicie kołowej na wysokości h1:
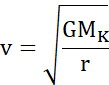
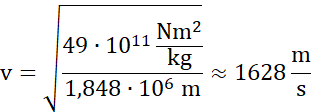
Promienie orbity eliptycznej:
![]()
![]()
Z poprzedniego podpunktu, podstawiając do wzoru na prędkość w peryselenium:
Za ra – ra1, rp – rp2
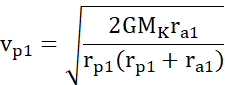
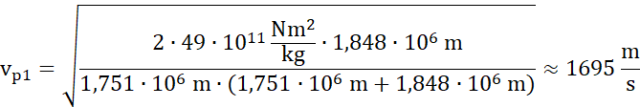
Z zasady zachowania momentu pędu mamy:
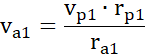
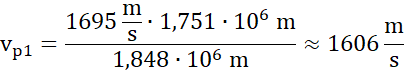
Jak zmieni się prędkość:
![]()
![]()
Prędkość spadła o około 22 metry na sekundę.

Peryselenium to miejsce, w którym znajduje się ciało niebieskie, kiedy znajduje się najbliżej Księżyca.
Aposelenium to miejsce, w którym znajduje się ciało niebieskie, kiedy znajduje się najdalej od Księżyca.
W tym zadaniu masz analogiczną sytuację, jak w poprzednim przykładzie, dlatego wyprowadzony wzór na prędkość dla różnych promieni możesz wykorzystać w tym przykładzie – zmieniając tylko promienie.

Zadanie 11.1.8.
16Zadanie 11.1.9.
17Zadanie 11.1.10.
17Zadanie 11.2.2.
21Zadanie 11.2.7.
25Zadanie 11.3.14.
33Zadanie 11.3.17.
34Zadanie 11.3.19.
35Zadanie 11.3.20.
35Zadanie 11.3.22.
35Zadanie 11.3.24.
36Zadanie 11.3.25.
36Zadanie 11.3.26.
36Zadanie 11.4.10.
44Zadanie 11.4.11.
44Zadanie 11.4.12.
44Zadanie 11.4.20.
46Zadanie 11.4.22.
46Zadanie 11.5.8.
54Zadanie 11.5.16.
57Zadanie 11.6.1.
66Zadanie 11.6.6.
67Zadanie 11.6.7.
67Zadanie 11.6.11.
68Zadanie 11.6.12.
69Zadanie 11.6.16.
69Zadanie 11.6.22.
70Zadanie 11.6.23.
71Zadanie 11.6.24.
71Zadanie 11.6.25.
71Zadanie 11.6.26.
72Zadanie 11.7.1.
74Zadanie 11.7.3.
75Zadanie 11.7.4.
75
